H11. Two Sum
Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.
You may assume that each input would have exactly one solution, and you may not use the same element twice.
You can return the answer in any order.
Example 1:
plaintext
Input: nums = [2,7,11,15], target = 9
Output: [0,1]
Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].Example 2:
plaintext
Input: nums = [3,2,4], target = 6
Output: [1,2]Example 3:
plaintext
Input: nums = [3,3], target = 6
Output: [0,1]Solution:
js
/**
* @param {number[]} nums
* @param {number} target
* @return {number[]}
*/
var twoSum = function(nums, target) {
const hash = new Map();
for (let i = 0; i < nums.length; i++) {
if (hash.has(nums[i])) return [hash.get(nums[i]), i];
hash.set(target - nums[i], i);
}
};H12. Add Two Numbers
You are given two non-empty linked lists representing two non-negative integers. The digits are stored in reverse order, and each of their nodes contains a single digit. Add the two numbers and return the sum as a linked list.
You may assume the two numbers do not contain any leading zero, except the number 0 itself.
Example 1:
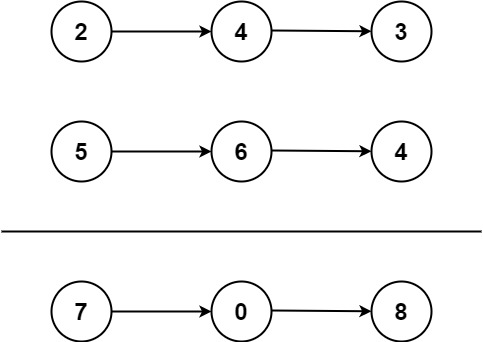
plaintext
Input: l1 = [2,4,3], l2 = [5,6,4]
Output: [7,0,8]
Explanation: 342 + 465 = 807.Solution:
js
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} l1
* @param {ListNode} l2
* @return {ListNode}
*/
var addTwoNumbers = function (l1, l2, carry = 0) {
if (!l1 && !l2 && !carry) return null;
const sum = (l1?.val || 0) + (l2?.val || 0) + carry;
return new ListNode(sum % 10, addTwoNumbers(l1?.next, l2?.next, sum > 9 ? 1 : 0));
};H13. Longest Substring Without Repeating Characters
Given a string s, find the length of the longest
substring
without repeating characters.
Example 1:
plaintext
Input: s = "abcabcbb"
Output: 3
Explanation: The answer is "abc", with the length of 3.Solution:
js
/**
* @param {string} s
* @return {number}
*/
var lengthOfLongestSubstring = function (s) {
if (!s) return 0;
let max = left = right = 0;
const map = new Map();
for (; right < s.length; right++) {
const index = map.get(s[right]);
if (index !== undefined && index >= left) {
left = index + 1;
}
map.set(s[right], right);
max = Math.max(max, right - left);
}
return max + 1;
};H114. Longest Common Prefix
Write a function to find the longest common prefix string amongst an array of strings.
If there is no common prefix, return an empty string "".
Example 1:
plaintext
Input: strs = ["flower","flow","flight"]
Output: "fl"Solution:
js
/**
* @param {string[]} strs
* @return {string}
*/
var longestCommonPrefix = function (strs) {
strs.sort();
const l = strs[0], r = strs[strs.length - 1];
let prefix = "";
for (let i = 0; i < l.length; i++) {
if (l[i] !== r[i]) break;
prefix += l[i];
}
return prefix;
};H119. Remove Nth Node From End of List
Given the head of a linked list, remove the nth node from the end of the list and return its head.
Example 1:
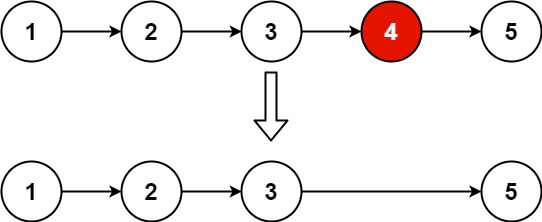
plaintext
Input: head = [1,2,3,4,5], n = 2
Output: [1,2,3,5]Solution:
js
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @param {number} n
* @return {ListNode}
*/
var removeNthFromEnd = function (head, n) {
let fast = slow = head;
for (let i = 0; i < n; i++) {
fast = fast.next;
}
if (!fast) {
return head.next;
}
while (fast.next) {
fast = fast.next;
slow = slow.next;
}
slow.next = slow.next.next;
return head;
};Note:
We use
fastandslowto reach the n^th^ node from the end of the list cleverly.
H121. Merge Two Sorted Lists
You are given the heads of two sorted linked lists list1 and list2.
Merge the two lists into one sorted list. The list should be made by splicing together the nodes of the first two lists.
Return the head of the merged linked list.
Example 1:
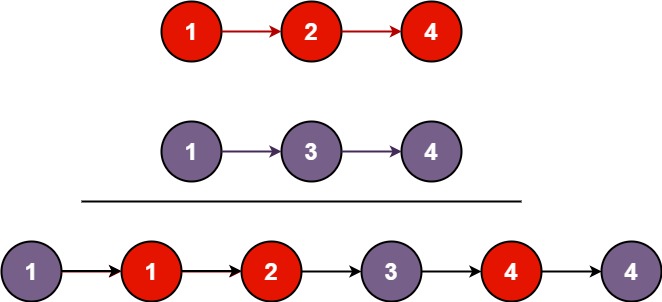
plaintext
Input: list1 = [1,2,4], list2 = [1,3,4]
Output: [1,1,2,3,4,4]Solution:
js
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} list1
* @param {ListNode} list2
* @return {ListNode}
*/
var mergeTwoLists = function (list1, list2) {
if (!list1) return list2;
if (!list2) return list1;
if (list1.val < list2.val) {
list1.next = mergeTwoLists(list1.next, list2);
return list1;
}
list2.next = mergeTwoLists(list1, list2.next);
return list2;
};H125. Reverse Nodes in k-Group
Given the head of a linked list, reverse the nodes of the list k at a time, and return the modified list.
k is a positive integer and is less than or equal to the length of the linked list. If the number of nodes is not a multiple of k then left-out nodes, in the end, should remain as it is.
You may not alter the values in the list's nodes, only nodes themselves may be changed.
Example 1:
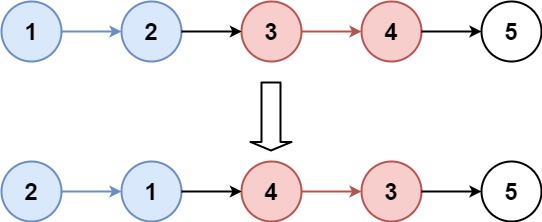
plaintext
Input: head = [1,2,3,4,5], k = 2
Output: [2,1,4,3,5]Solution:
js
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @param {number} k
* @return {ListNode}
*/
var reverseKGroup = function (head, k) {
if (!head) return null;
let tail = head;
for (let i = 1; i < k; i++) {
tail = tail.next;
if (!tail) return head;
}
let next = tail.next;
tail.next = null;
// Reverse
let prev, curr = head;
while (curr) {
let temp = curr;
curr = curr.next;
temp.next = prev;
prev = temp;
}
head.next = reverseKGroup(next, k);
return tail;
};H126. Remove Duplicates from Sorted Array
Given an integer array nums sorted in non-decreasing order, remove the duplicates in-place such that each unique element appears only once. The relative order of the elements should be kept the same. Then return the number of unique elements in nums.
Consider the number of unique elements of nums to be k, to get accepted, you need to do the following things:
- Change the array
numssuch that the firstkelements ofnumscontain the unique elements in the order they were present innumsinitially. The remaining elements ofnumsare not important as well as the size ofnums. - Return
k.
Example 1:
plaintext
Input: nums = [1,1,2]
Output: 2, nums = [1,2,_]
Explanation: Your function should return k = 2, with the first two elements of nums being 1 and 2 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).Constraints:
1 <= nums.length <= 3 * 104-100 <= nums[i] <= 100numsis sorted in non-decreasing order.
Solution:
js
/**
* @param {number[]} nums
* @return {number}
*/
var removeDuplicates = function (nums) {
let count = 1, i = 0;
for (let j = 1; j < nums.length; j++) {
if (nums[i] === nums[j]) {
nums[j] = 101;
} else {
i = j;
count++;
}
}
nums.sort((a, b) => a - b);
return count;
}Note: We ought to use a two-pointer approach here. One, that would keep track of the current element in the original array and another one for just the unique elements.
H133. Search in Rotated Sorted Array
There is an integer array nums sorted in ascending order (with distinct values).
Prior to being passed to your function, nums is possibly rotated at an unknown pivot index k (1 <= k < nums.length) such that the resulting array is [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]] (0-indexed). For example, [0,1,2,4,5,6,7] might be rotated at pivot index 3 and become [4,5,6,7,0,1,2].
Given the array nums after the possible rotation and an integer target, return the index of target if it is in nums, or -1 if it is not in nums.
You must write an algorithm with O(log n) runtime complexity.
Example 1:
plaintext
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4Example 2:
plaintext
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1Solution:
js
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var search = function (nums, target) {
let l = 0, r = nums.length - 1;
if (nums[0] === target) return 0;
if (nums.at(-1) === target) return r;
while (l <= r) {
const m = Math.floor((l + r) / 2);
if (nums[m] === target) {
return m;
} else if (nums[l] <= nums[m]) {
if (nums[l] <= target && target < nums[m]) {
r = m - 1;
} else {
l = m + 1;
}
} else {
if (nums[m] < target && target <= nums[r]) {
l = m + 1;
} else {
r = m - 1;
}
}
}
return -1;
};H145. Jump Game II
You are given a 0-indexed array of integers nums of length n. You are initially positioned at nums[0].
Each element nums[i] represents the maximum length of a forward jump from index i. In other words, if you are at nums[i], you can jump to any nums[i + j] where:
0 <= j <= nums[i]andi + j < n
Return the minimum number of jumps to reach nums[n - 1]. The test cases are generated such that you can reach nums[n - 1].
Example 1:
plaintext
Input: nums = [2,3,1,1,4]
Output: 2
Explanation: The minimum number of jumps to reach the last index is 2. Jump 1 step from index 0 to 1, then 3 steps to the last index.Solution:
js
/**
* @param {number[]} nums
* @return {number}
*/
var jump = function (nums) {
const len = nums.length - 1;
let l = -1, r = 0, res = 0;
for (let i = 0; r < len; i++) {
if (l < i) l = r, res++;
r = Math.max(r, i + nums[i]);
}
return res;
};H149. Group Anagrams
Given an array of strings strs, group the anagrams together. You can return the answer in any order.
An Anagram is a word or phrase formed by rearranging the letters of a different word or phrase, typically using all the original letters exactly once.
Example 1:
plaintext
Input: strs = ["eat","tea","tan","ate","nat","bat"]
Output: [["bat"],["nat","tan"],["ate","eat","tea"]]Solution:
js
/**
* @param {string[]} strs
* @return {string[][]}
*/
var groupAnagrams = function (strs) {
const hash = new Map();
for (const str of strs) {
const str1 = [...str].sort().join("");
if (!hash.has(str1)) hash.set(str1, []);
hash.get(str1).push(str);
}
return Array.from(hash.values());
};Note: In scenarios where key-value pairs are frequently added or deleted,
Mapmay perform better thanObject.
H153. Maximum Subarray
Given an integer array nums, find the subarray with the largest sum, and return its sum.
Example 1:
plaintext
Input: nums = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: The subarray [4,-1,2,1] has the largest sum 6.Solution:
js
/**
* @param {number[]} nums
* @return {number}
*/
var maxSubArray = function(nums) {
let max = nums[0];
for (let i = 1; i < nums.length; i++) {
nums[i] = nums[i] + Math.max(0, nums[i - 1]);
if (nums[i] > max) max = nums[i];
}
return max;
};Note:
dp[i] = nums[i] + max(0, dp[i-1])
H154. Spiral Matrix
Given an m x n matrix, return all elements of the matrix in spiral order.
Example 1:

plaintext
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]Solution:
js
/**
* @param {number[][]} matrix
* @return {number[]}
*/
var spiralOrder = function (matrix) {
const res = [];
let left = top = 0, bottom = matrix.length - 1, right = matrix[0].length - 1;
while (left <= right && top <= bottom) {
for (let j = left; j <= right; j++) {
res.push(matrix[top][j]);
}
top++;
for (let i = top; i <= bottom; i++) {
res.push(matrix[i][right]);
}
right--;
if (top <= bottom) {
for (let j = right; j >= left; j--) {
res.push(matrix[bottom][j]);
}
bottom--;
}
if (left <= right) {
for (let i = bottom; i >= top; i--) {
res.push(matrix[i][left]);
}
left++;
}
}
return res;
};H155. Jump Game
You are given an integer array nums. You are initially positioned at the array's first index, and each element in the array represents your maximum jump length at that position.
Return true if you can reach the last index, or false otherwise.
Example 1:
plaintext
Input: nums = [2,3,1,1,4]
Output: true
Explanation: Jump 1 step from index 0 to 1, then 3 steps to the last index.Solution:
js
/**
* @param {number[]} nums
* @return {boolean}
*/
var canJump = function (nums) {
if (nums.length === 1) return true;
for (var i = nums.length - 2, j = nums.length - 1; i >= 0; i--) {
if (nums[i] >= j - i) j = i;
}
return j ? false : true;
};H157. Insert Interval
You are given an array of non-overlapping intervals intervals where intervals[i] = [starti, endi] represent the start and the end of the ith interval and intervals is sorted in ascending order by starti. You are also given an interval newInterval = [start, end] that represents the start and end of another interval.
Insert newInterval into intervals such that intervals is still sorted in ascending order by starti and intervals still does not have any overlapping intervals (merge overlapping intervals if necessary).
Return intervals after the insertion.
Note that you don't need to modify intervals in-place. You can make a new array and return it.
Example 1:
plaintext
Input: intervals = [[1,3],[6,9]], newInterval = [2,5]
Output: [[1,5],[6,9]]Solution:
js
/**
* @param {number[][]} intervals
* @param {number[]} newInterval
* @return {number[][]}
*/
var insert = function (intervals, newInterval) {
const res = [];
for (let interval of intervals) {
if (!newInterval || interval[1] < newInterval[0]) {
res.push(interval);
} else if (newInterval[1] < interval[0]) {
res.push(newInterval, interval);
newInterval = null;
} else {
newInterval[0] = Math.min(newInterval[0], interval[0]);
newInterval[1] = Math.max(newInterval[1], interval[1]);
}
}
if (newInterval) {
res.push(newInterval);
}
return res;
};H171. Simplify Path
Given a string path, which is an absolute path (starting with a slash '/') to a file or directory in a Unix-style file system, convert it to the simplified canonical path.
In a Unix-style file system, a period '.' refers to the current directory, a double period '..' refers to the directory up a level, and any multiple consecutive slashes (i.e. '//') are treated as a single slash '/'. For this problem, any other format of periods such as '...' are treated as file/directory names.
The canonical path should have the following format:
- The path starts with a single slash
'/'. - Any two directories are separated by a single slash
'/'. - The path does not end with a trailing
'/'. - The path only contains the directories on the path from the root directory to the target file or directory (i.e., no period
'.'or double period'..')
Return the simplified canonical path.
Example 1:
plaintext
Input: path = "/home/"
Output: "/home"
Explanation: Note that there is no trailing slash after the last directory name.Example 2:
plaintext
Input: path = "/../"
Output: "/"
Explanation: Going one level up from the root directory is a no-op, as the root level is the highest level you can go.Solution:
js
/**
* @param {string} path
* @return {string}
*/
var simplifyPath = function (path) {
const stack = [];
for (const p of path.split("/")) {
if (p === "..") {
stack.pop();
} else if (p && p !== ".") {
stack.push(p);
}
}
return "/" + stack.join("/");
};H180. Remove Duplicates from Sorted Array II
Given an integer array nums sorted in non-decreasing order, remove some duplicates in-place such that each unique element appears at most twice. The relative order of the elements should be kept the same.
Since it is impossible to change the length of the array in some languages, you must instead have the result be placed in the first part of the array nums. More formally, if there are k elements after removing the duplicates, then the first k elements of nums should hold the final result. It does not matter what you leave beyond the first k elements.
Return k after placing the final result in the first k slots of nums.
Do not allocate extra space for another array. You must do this by modifying the input array in-place with O(1) extra memory.
Example 1:
plaintext
Input: nums = [1,1,1,2,2,3]
Output: 5, nums = [1,1,2,2,3,_]
Explanation: Your function should return k = 5, with the first five elements of nums being 1, 1, 2, 2 and 3 respectively.
It does not matter what you leave beyond the returned k (hence they are underscores).Solution:
js
/**
* @param {number[]} nums
* @return {number}
*/
var removeDuplicates = function (nums) {
if (nums.length <= 2) {
return nums.length;
}
for (var i = j = 2; j < nums.length; j++) {
if (nums[j] != nums[i - 2] || nums[j] != nums[i - 1]) {
nums[i] = nums[j];
i++;
}
}
return i;
};H188. Merge Sorted Array
You are given two integer arrays nums1 and nums2, sorted in non-decreasing order, and two integers m and n, representing the number of elements in nums1 and nums2 respectively.
Merge nums1 and nums2 into a single array sorted in non-decreasing order.
The final sorted array should not be returned by the function, but instead be stored inside the array nums1. To accommodate this, nums1 has a length of m + n, where the first m elements denote the elements that should be merged, and the last n elements are set to 0 and should be ignored. nums2 has a length of n.
Example 1:
plaintext
Input: nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
Output: [1,2,2,3,5,6]
Explanation: The arrays we are merging are [1,2,3] and [2,5,6].
The result of the merge is [1,2,2,3,5,6] with the underlined elements coming from nums1.Solution:
js
/**
* @param {number[]} nums1
* @param {number} m
* @param {number[]} nums2
* @param {number} n
* @return {void} Do not return anything, modify nums1 in-place instead.
*/
var merge = function (nums1, m, nums2, n) {
m--;
n--;
while (n >= 0) {
if (m >= 0 && (nums1[m] > nums2[n])) {
nums1[m + n + 1] = nums1[m];
m--;
} else {
nums1[m + n + 1] = nums2[n];
n--;
}
}
};H192. Reverse Linked List II
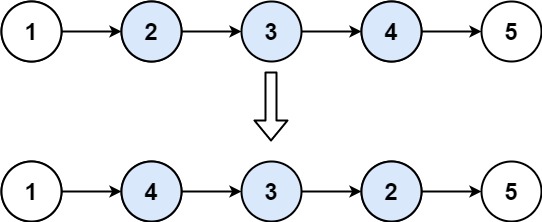
Given the head of a singly linked list and two integers left and right where left <= right, reverse the nodes of the list from position left to position right, and return the reversed list.
Example 1:
plaintext
Input: head = [1,2,3,4,5], left = 2, right = 4
Output: [1,4,3,2,5]Solution:
js
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @param {number} left
* @param {number} right
* @return {ListNode}
*/
var reverseBetween = function (head, left, right) {
if (!head?.next || left === right) return head;
let i = 1, curr = next = head, prev = null;
while (i < left) {
[prev, curr] = [curr, curr.next];
i++;
}
let prev1 = prev, curr1 = curr;
while (i <= right) {
next = curr.next;
curr.next = prev;
prev = curr;
curr = next;
i++;
}
if (left > 1) {
prev1.next = prev;
} else {
head = prev;
}
curr1.next = curr;
return head;
};H1100. Same Tree
Given the roots of two binary trees p and q, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
Example 1:
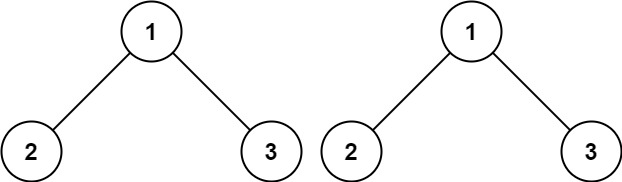
plaintext
Input: p = [1,2,3], q = [1,2,3]
Output: trueSolution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} p
* @param {TreeNode} q
* @return {boolean}
*/
var isSameTree = function (p, q) {
if (p === null && q === null) return true;
if (!p || !q) return false;
if (p.val === q.val) return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
return false;
};H1101. Symmetric Tree
Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).
Example 1:
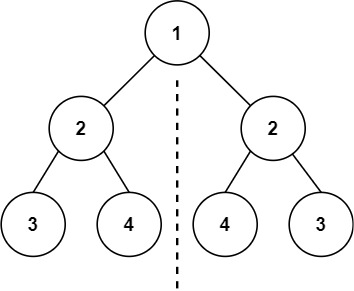
plaintext
Input: root = [1,2,2,3,4,4,3]
Output: trueSolution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {boolean}
*/
var isSymmetric = function (root) {
const q = [root.left, root.right];
while (q.length) {
const l = q.shift(), r = q.shift();
if (!l && !r) continue;
if (!l || !r || l.val !== r.val) return false;
q.push(l.right, r.left, l.left, r.right);
}
return true;
};H1102. Binary Tree Level Order Traversal
Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).
Example 1:
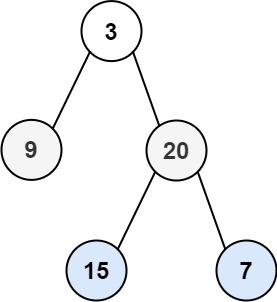
plaintext
Input: root = [3,9,20,null,null,15,7]
Output: [[3],[9,20],[15,7]]Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[][]}
*/
var levelOrder = function (root) {
if (!root) return [];
const res = [], q = [root];
while (q.length) {
res.push([]);
let len = q.length;
while (len) {
const node = q.shift();
res.at(-1).push(node.val);
if (node.left) q.push(node.left);
if (node.right) q.push(node.right);
len--;
}
}
return res;
};H1112. Path Sum
Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.
A leaf is a node with no children.
Example 1:
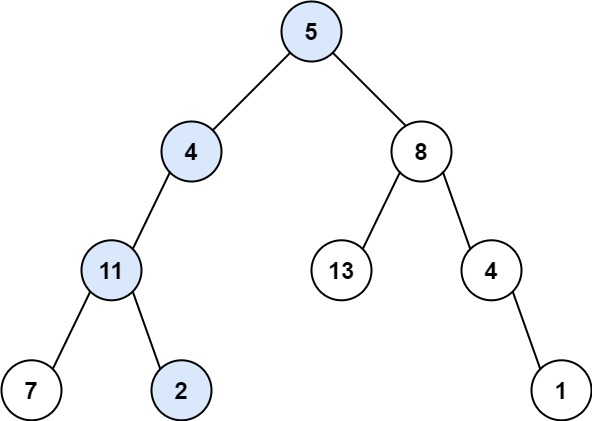
plaintext
Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true
Explanation: The root-to-leaf path with the target sum is shown.Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} targetSum
* @return {boolean}
*/
var hasPathSum = function (root, targetSum) {
if (!root) return false;
if (root.val === targetSum && !root.left && !root.right) return true;
return hasPathSum(root.left, targetSum - root.val) || hasPathSum(root.right, targetSum - root.val);
};H1114. Flatten Binary Tree to Linked List
Given the root of a binary tree, flatten the tree into a "linked list":
- The "linked list" should use the same
TreeNodeclass where therightchild pointer points to the next node in the list and theleftchild pointer is alwaysnull. - The "linked list" should be in the same order as a pre-order traversal of the binary tree.
Example 1:
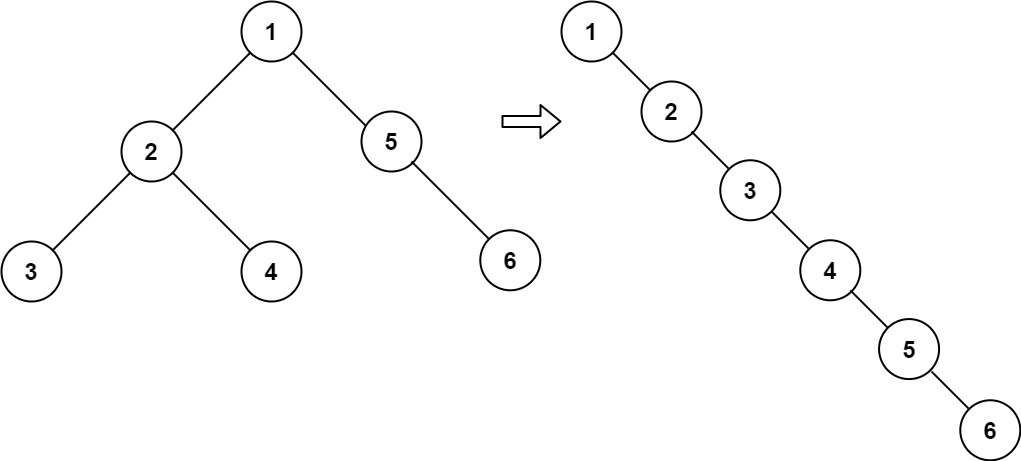
plaintext
Input: root = [1,2,5,3,4,null,6]
Output: [1,null,2,null,3,null,4,null,5,null,6]Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {void} Do not return anything, modify root in-place instead.
*/
var flatten = function (root) {
let crt = root;
while (crt) {
if (crt.left) {
let runner = crt.left;
while (runner.right) runner = runner.right;
runner.right = crt.right;
crt.right = crt.left;
crt.left = null;
}
crt = crt.right;
}
};Note: Here we use
Morris Traversal.
H1108. Convert Sorted Array to Binary Search Tree
Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.
Example 1:
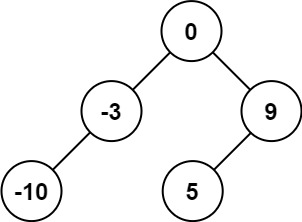
plaintext
Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]
Explanation: [0,-10,5,null,-3,null,9] is also accepted:Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {number[]} nums
* @return {TreeNode}
*/
var sortedArrayToBST = function (nums) {
const dfs = (beg, end) => {
if (beg > end) return null;
const mid = Math.floor((beg + end) / 2);
const node = new TreeNode(nums[mid]);
node.left = dfs(beg, mid - 1);
node.right = dfs(mid + 1, end);
return node;
}
return dfs(0, nums.length - 1);
};H1117. Populating Next Right Pointers in Each Node II
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Example 1:
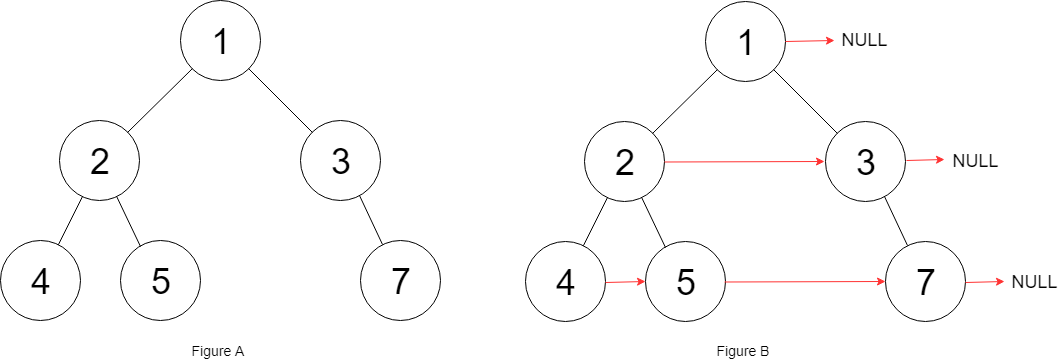
plaintext
Input: root = [1,2,3,4,5,null,7]
Output: [1,#,2,3,#,4,5,7,#]Solution:
js
/**
* // Definition for a Node.
* function Node(val, left, right, next) {
* this.val = val === undefined ? null : val;
* this.left = left === undefined ? null : left;
* this.right = right === undefined ? null : right;
* this.next = next === undefined ? null : next;
* };
*/
/**
* @param {Node} root
* @return {Node}
*/
var connect = function (root) {
if (!root) return null;
const q = [[root, 0]];
while (q.length) {
const [curr, level] = q.shift();
if (q.length) {
const [next, nextLevel] = q[0];
if (level === nextLevel) curr.next = next;
}
if (curr.left) q.push([curr.left, level + 1]);
if (curr.right) q.push([curr.right, level + 1]);
}
return root;
};H1121. Best Time to Buy and Sell Stock
You are given an array prices where prices[i] is the price of a given stock on the ith day.
You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
Example 1:
plaintext
Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.Example 2:
plaintext
Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.Solution:
js
/**
* @param {number[]} prices
* @return {number}
*/
var maxProfit = function (prices) {
let min = prices[0], profit = 0;
for (let i = 0; i < prices.length; i++) {
if (min > prices[i]) {
min = prices[i];
} else if (prices[i] - min > profit) {
profit = prices[i] - min;
}
}
return profit;
};H1128. Longest Consecutive Sequence
Given an unsorted array of integers nums, return the length of the longest consecutive elements sequence.
You must write an algorithm that runs in O(n) time.
Example 1:
plaintext
Input: nums = [100,4,200,1,3,2]
Output: 4
Explanation: The longest consecutive elements sequence is [1, 2, 3, 4]. Therefore its length is 4.Solution:
js
/**
* @param {number[]} nums
* @return {number}
*/
var longestConsecutive = function (nums) {
const set = new Set(nums);
let max = 0;
for (const n of [...set]) {
if (!set.has(n - 1)) {
let len = 1;
while (set.has(n + len)) len++;
max = Math.max(max, len)
}
}
return max;
};Note: Every number will be accessed at most twice, so the time complexity is
O(n).
H1130. Surrounded Regions
Given an m x n matrix board containing 'X' and 'O', capture all regions that are 4-directionally surrounded by 'X'.
A region is captured by flipping all 'O's into 'X's in that surrounded region.
Example 1:

plaintext
Input: board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
Output: [["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
Explanation: Notice that an 'O' should not be flipped if:
- It is on the border, or
- It is adjacent to an 'O' that should not be flipped.
The bottom 'O' is on the border, so it is not flipped.
The other three 'O' form a surrounded region, so they are flipped.Solution:
js
/**
* @param {character[][]} board
* @return {void} Do not return anything, modify board in-place instead.
*/
var solve = function (board) {
const m = board.length, n = board[0].length;
const dfs = (i, j) => {
if (0 > i || i >= m || 0 > j || j >= n) return;
if (board[i][j] === "O") {
board[i][j] = "S"
dfs(i + 1, j);
dfs(i - 1, j);
dfs(i, j + 1);
dfs(i, j - 1);
}
}
for (let i = 0; i < m; i++) {
for (let j = 0; j < n;) {
if (board[i][j] === "O") dfs(i, j);
if (!i || i === m - 1) {
j++;
} else {
j += n - 1;
}
}
}
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
board[i][j] = board[i][j] === "O" ? "X" : board[i][j] === "S" ? "O" : "X";
}
}
};Note:
- We have to traverse
board's boader once to find "O".- If we find "O", run dfs on this "O" and rename all the adjacent "O" as "S" which stands for "Saving".
- Traverse
boardagain to rename all the "O" as "X" and "S" as "O".
H1133. Clone Graph
Given a reference of a node in a connected undirected graph.
Return a deep copy (clone) of the graph.
Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.
plaintext
class Node {
public int val;
public List<Node> neighbors;
} Test case format:
For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.
An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.
The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.
Example 1:
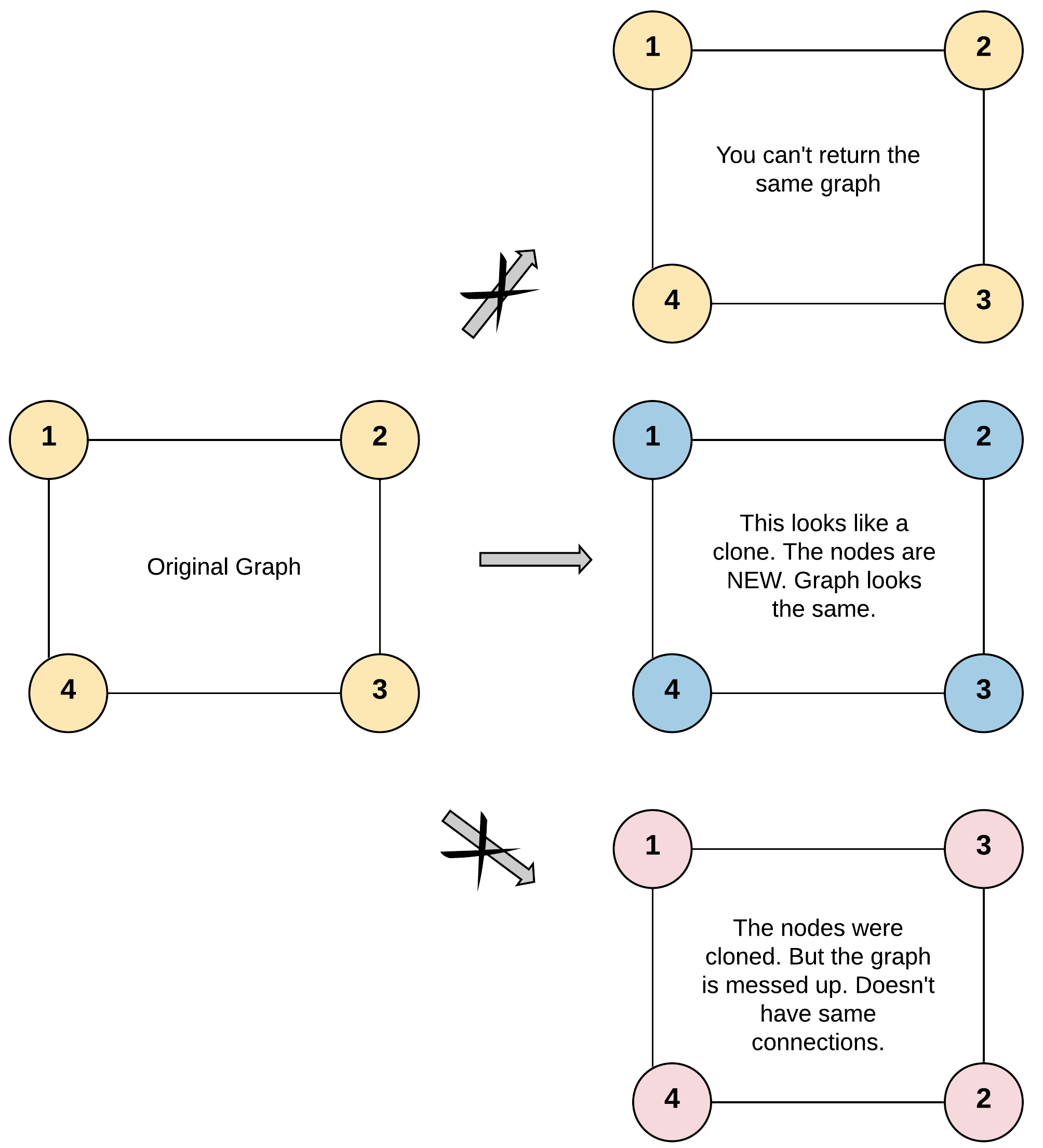
plaintext
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).Solution:
js
/**
* // Definition for a Node.
* function Node(val, neighbors) {
* this.val = val === undefined ? 0 : val;
* this.neighbors = neighbors === undefined ? [] : neighbors;
* };
*/
/**
* @param {Node} node
* @return {Node}
*/
var cloneGraph = function (graph) {
if (!graph) return null;
const map = new Map();
const dfs = (node) => {
if (!map.has(node.val)) {
map.set(node.val, new Node(node.val));
map.get(node.val).neighbors = node.neighbors.map(dfs); // Key Point
}
return map.get(node.val);
}
return dfs(graph);
};H1134. Gas Station
There are n gas stations along a circular route, where the amount of gas at the ith station is gas[i].
You have a car with an unlimited gas tank and it costs cost[i] of gas to travel from the ith station to its next (i + 1)th station. You begin the journey with an empty tank at one of the gas stations.
Given two integer arrays gas and cost, return the starting gas station's index if you can travel around the circuit once in the clockwise direction, otherwise return -1. If there exists a solution, it is guaranteed to be unique
Example 1:
plaintext
Input: gas = [1,2,3,4,5], cost = [3,4,5,1,2]
Output: 3
Explanation:
Start at station 3 (index 3) and fill up with 4 unit of gas. Your tank = 0 + 4 = 4
Travel to station 4. Your tank = 4 - 1 + 5 = 8
Travel to station 0. Your tank = 8 - 2 + 1 = 7
Travel to station 1. Your tank = 7 - 3 + 2 = 6
Travel to station 2. Your tank = 6 - 4 + 3 = 5
Travel to station 3. The cost is 5. Your gas is just enough to travel back to station 3.
Therefore, return 3 as the starting index.Solution:
js
/**
* @param {number[]} gas
* @param {number[]} cost
* @return {number}
*/
var canCompleteCircuit = function (gas, cost) {
let start = 0, tank = 0, totalTank = 0;
for (let i = 0; i < gas.length; i++) {
const netCost = gas[i] - cost[i];
totalTank += netCost;
tank += netCost;
if (tank < 0) {
tank = 0;
start = i + 1;
}
}
return totalTank < 0 ? -1 : start;
};H1135. Candy
There are n children standing in a line. Each child is assigned a rating value given in the integer array ratings.
You are giving candies to these children subjected to the following requirements:
- Each child must have at least one candy.
- Children with a higher rating get more candies than their neighbors.
Return the minimum number of candies you need to have to distribute the candies to the children.
Example 1:
plaintext
Input: ratings = [1,0,2]
Output: 5
Explanation: You can allocate to the first, second and third child with 2, 1, 2 candies respectively.Solution:
js
/**
* @param {number[]} ratings
* @return {number}
*/
var candy = function (ratings) {
const len = ratings.length, candy = Array(len).fill(1);
for (let i = 1; i < len; i++) {
if (ratings[i - 1] < ratings[i]) {
candy[i] = candy[i - 1] + 1;
}
}
for (let i = len - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) {
candy[i] = Math.max(candy[i], candy[i + 1] + 1);
}
}
return candy.reduce((a, c) => a + c);
};Note:
- Initialize
Candiesarray filled with 1.- Conduct Forward pass & Backward pass to ensure the current candy number is less than or more neighbor candy numbers based on comparison.
- Sum it all up.
H1138. Copy List with Random Pointer
A linked list of length n is given such that each node contains an additional random pointer, which could point to any node in the list, or null.
Construct a deep copy of the list. The deep copy should consist of exactly n brand new nodes, where each new node has its value set to the value of its corresponding original node. Both the next and random pointer of the new nodes should point to new nodes in the copied list such that the pointers in the original list and copied list represent the same list state. None of the pointers in the new list should point to nodes in the original list.
For example, if there are two nodes X and Y in the original list, where X.random --> Y, then for the corresponding two nodes x and y in the copied list, x.random --> y.
Return the head of the copied linked list.
The linked list is represented in the input/output as a list of n nodes. Each node is represented as a pair of [val, random_index] where:
val: an integer representingNode.valrandom_index: the index of the node (range from0ton-1) that therandompointer points to, ornullif it does not point to any node.
Your code will only be given the head of the original linked list.
Example 1:
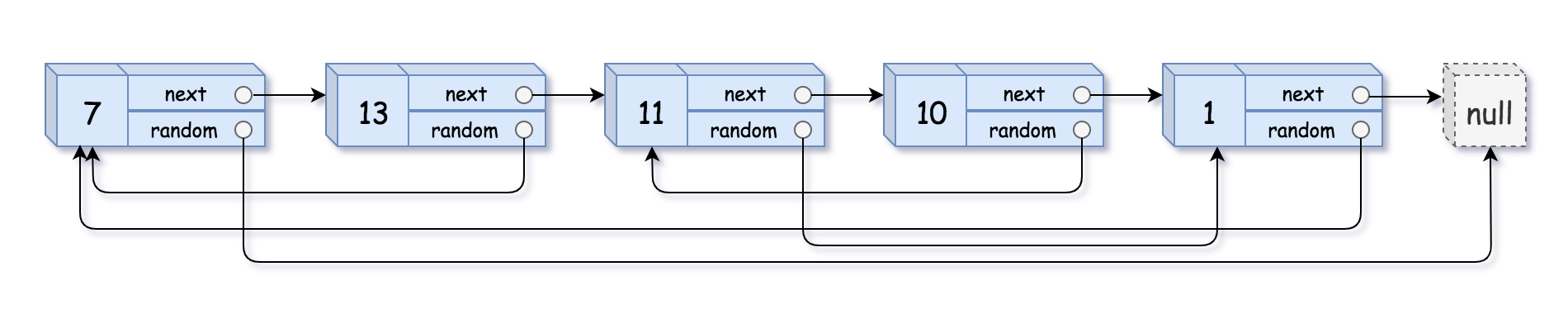
plaintext
Input: head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
Output: [[7,null],[13,0],[11,4],[10,2],[1,0]]Solution
js
/**
* // Definition for a Node.
* function Node(val, next, random) {
* this.val = val;
* this.next = next;
* this.random = random;
* };
*/
/**
* @param {Node} head
* @return {Node}
*/
var copyRandomList = function(head) {
if (!head) return null;
const oldToNew = new Map();
let curr = head;
while (curr) {
oldToNew.set(curr, new Node(curr.val));
curr = curr.next;
}
curr = head;
while (curr) {
oldToNew.get(curr).next = oldToNew.get(curr.next) || null;
oldToNew.get(curr).random = oldToNew.get(curr.random) || null;
curr = curr.next;
}
return oldToNew.get(head);
};H1141. Linked List Cycle
Given head, the head of a linked list, determine if the linked list has a cycle in it.
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail's next pointer is connected to. Note that pos is not passed as a parameter.
Return true if there is a cycle in the linked list. Otherwise, return false.
Example 1:
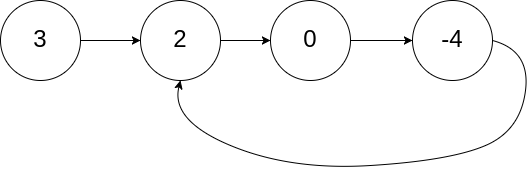
plaintext
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).Solution:
js
/**
* Definition for singly-linked list.
* function ListNode(val) {
* this.val = val;
* this.next = null;
* }
*/
/**
* @param {ListNode} head
* @return {boolean}
*/
var hasCycle = function(head) {
let s = head, i = 0;
while (head) {
head = head.next;
if (s === head) return true;
if (i++ % 2 === 1) s = s.next;
}
return false;;
};H1162. Find Peak Element
A peak element is an element that is strictly greater than its neighbors.
Given a 0-indexed integer array nums, find a peak element, and return its index. If the array contains multiple peaks, return the index to any of the peaks.
You may imagine that nums[-1] = nums[n] = -∞. In other words, an element is always considered to be strictly greater than a neighbor that is outside the array.
You must write an algorithm that runs in O(log n) time.
Example 1:
plaintext
Input: nums = [1,2,3,1]
Output: 2
Explanation: 3 is a peak element and your function should return the index number 2.Solution:
js
/**
* @param {number[]} nums
* @return {number}
*/
var findPeakElement = function (nums) {
let l = 0, r = nums.length - 1;
if (nums.length === 1 || nums[0] > nums[1]) return 0;
if (nums[r] > nums[r - 1]) return r;
while (l <= r) {
const m = Math.floor((l + r) / 2);
if (nums[m - 1] < nums[m] && nums[m + 1] < nums[m]) {
return m;
} else if (nums[m] > nums[m + 1]) {
r = m - 1;
} else {
l = m + 1;
}
}
};H1169. Majority Element
Given an array nums of size n, return the majority element.
The majority element is the element that appears more than ⌊n / 2⌋ times. You may assume that the majority element always exists in the array.
Example 1:
plaintext
Input: nums = [3,2,3]
Output: 3Solution:
js
/**
* @param {number[]} nums
* @return {number}
*/
var majorityElement = function (nums) {
let candidate, vote = 0;
for (const n of nums) {
if (candidate === n) {
vote++;
} else {
if (vote === 0) {
candidate = n;
} else {
vote--;
}
}
}
return candidate;
};Note: Use Boyer-Moore Voting Algorithm.
H1199. Binary Tree Right Side View
Given the root of a binary tree, imagine yourself standing on the right side of it, return the values of the nodes you can see ordered from top to bottom.
Example 1:

plaintext
Input: root = [1,2,3,null,5,null,4]
Output: [1,3,4]Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var rightSideView = function (root) {
const res = [], v = new Set();
const dfs = (node, i) => {
if (!node) return;
if (!v.has(i)) {
v.add(i);
res.push(node.val);
}
dfs(node.right, i + 1);
dfs(node.left, i + 1);
}
dfs(root, 0);
return res;
};H1200. Number of Islands
Given an m x n 2D binary grid grid which represents a map of '1's (land) and '0's (water), return the number of islands.
An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example 1:
plaintext
Input: grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
Output: 1Solution:
js
/**
* @param {character[][]} grid
* @return {number}
*/
var numIslands = function (grid) {
// const m = grid.length, n = grid[0].length;
// const v = Array.from({ length: m }, () => new Array(n).fill(0));
// const moves = [[0, 1], [0, -1], [1, 0], [-1, 0]];
// let count = 0;
// for (let i = 0; i < m; i++) {
// for (let j = 0; j < n; j++) {
// if (!v[i][j] && +grid[i][j]) {
// v[i][j] = 1;
// const q = [[i, j]];
// while (q.length) {
// const [x, y] = q.shift();
// for (const [mx, my] of moves) {
// const newX = x + mx, newY = y + my;
// if (0 <= newX && newX < m && 0 <= newY && newY < n && !v[newX][newY] && +grid[newX][newY]) {
// v[newX][newY] = 1;
// q.push([newX, newY]);
// }
// }
// }
// count++;
// }
// }
// }
// return count;
const m = grid.length, n = grid[0].length;
let count = 0;
const dfs = (x, y) => {
if (0 > x || x >= m || 0 > y || y >= n || !+grid[x][y]) return;
grid[x][y] = "0"; // Key Point
dfs(x - 1, y);
dfs(x + 1, y);
dfs(x, y - 1);
dfs(x, y + 1);
}
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (+grid[i][j]) dfs(i, j), count++;
}
}
return count;
};H1206. Reverse Linked List
Given the head of a singly linked list, reverse the list, and return the reversed list.
Example 1:

plaintext
Input: head = [1,2,3,4,5]
Output: [5,4,3,2,1]Solution:
js
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var reverseList = function(head) {
let result = null;
while (head) {
const nextNode = head.next;
head.next = result;
result = head;
head = nextNode;
}
return result;
};H1207. Course Schedule
There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.
- For example, the pair
[0, 1], indicates that to take course0you have to first take course1.
Return true if you can finish all courses. Otherwise, return false.
Example 1:
plaintext
Input: numCourses = 2, prerequisites = [[1,0]]
Output: true
Explanation: There are a total of 2 courses to take.
To take course 1 you should have finished course 0. So it is possible.Solution:
js
/**
* @param {number} numCourses
* @param {number[][]} prerequisites
* @return {boolean}
*/
var canFinish = function (numCourses, prerequisites) {
const v = new Set(), adj = Array.from({ length: numCourses }, () => []);
for (const [x, y] of prerequisites) adj[x].push(y);
// Can this course be finished?
const dfs = (node) => {
if (v.has(node)) return false;
if (!adj[node].length) return true;
v.add(node);
for (const n of adj[node]) if (!dfs(n)) return false;
// If nothing happens, that means this is acyclic. The couse can be taken.
v.delete(node);
adj[node] = [];
return true;
}
for (let i = 0; i < numCourses; i++) {
if (!dfs(i)) return false;
}
return true;
};Note:
H1209. Minimum Size Subarray Sum
Given an array of positive integers nums and a positive integer target, return the minimal length of a
subarray
whose sum is greater than or equal to target. If there is no such subarray, return 0 instead.
Example 1:
plaintext
Input: target = 7, nums = [2,3,1,2,4,3]
Output: 2
Explanation: The subarray [4,3] has the minimal length under the problem constraint.Example 2:
plaintext
Input: target = 4, nums = [1,4,4]
Output: 1Solution:
js
/**
* @param {number} target
* @param {number[]} nums
* @return {number}
*/
var minSubArrayLen = function (target, nums) {
let i = j = sum = 0, min = Infinity;
while (j < nums.length || sum >= target) {
if (sum >= target) {
min = Math.min(min, j - i);
sum -= nums[i];
i++;
} else {
sum += nums[j];
j++;
}
}
return min === Infinity ? 0 : min;
};H1228. Summary Ranges
You are given a sorted unique integer array nums.
A range [a,b] is the set of all integers from a to b (inclusive).
Return the smallest sorted list of ranges that cover all the numbers in the array exactly. That is, each element of nums is covered by exactly one of the ranges, and there is no integer x such that x is in one of the ranges but not in nums.
Each range [a,b] in the list should be output as:
"a->b"ifa != b"a"ifa == b
Example 1:
plaintext
Input: nums = [0,1,2,4,5,7]
Output: ["0->2","4->5","7"]
Explanation: The ranges are:
[0,2] --> "0->2"
[4,5] --> "4->5"
[7,7] --> "7"Solution:
js
/**
* @param {number[]} nums
* @return {string[]}
*/
var summaryRanges = function (nums) {
const res = [];
for (let i = 0, left = nums[0]; i < nums.length; i++) {
if (nums[i] + 1 !== nums[i + 1]) {
res.push(left === nums[i] ? String(nums[i]) : left + "->" + nums[i]);
left = nums[i + 1];
}
}
return res;
};H1236. Lowest Common Ancestor of a Binary Tree
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Example 1:

plaintext
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} root
* @param {TreeNode} p
* @param {TreeNode} q
* @return {TreeNode}
*/
var lowestCommonAncestor = function (root, p, q) {
if (!root || root === p || root === q) return root;
const left = lowestCommonAncestor(root.left, p, q);
const right = lowestCommonAncestor(root.right, p, q);
return (left && right) ? root : (left || right);
};H1238. Product of Array Except Self
Given an integer array nums, return an array answer such that answer[i] is equal to the product of all the elements of nums except nums[i].
The product of any prefix or suffix of nums is guaranteed to fit in a 32-bit integer.
You must write an algorithm that runs in O(n) time and without using the division operation.
Example 1:
plaintext
Input: nums = [1,2,3,4]
Output: [24,12,8,6]Solution:
js
/**
* @param {number[]} nums
* @return {number[]}
*/
var productExceptSelf = function(nums) {
const len = nums.length, arr = [1];
for (let i = 1; i < len; i++) {
arr[i] = arr[i - 1] * nums[i - 1];
}
let suf = nums[len - 1];
for (let i = len - 2; i > -1; i--) {
arr[i] *= suf;
suf *= nums[i];
}
return arr;
};H1283. Move Zeroes
Given an integer array nums, move all 0's to the end of it while maintaining the relative order of the non-zero elements.
Note that you must do this in-place without making a copy of the array.
Example 1:
plaintext
Input: nums = [0,1,0,3,12]
Output: [1,3,12,0,0]Solution:
js
/**
* @param {number[]} nums
* @return {void} Do not return anything, modify nums in-place instead.
*/
var moveZeroes = function (nums) {
for (let i = j = 0; i < nums.length; i++) {
if (nums[i] !== 0) {
[nums[i], nums[j]] = [nums[j], nums[i]];
j++;
}
}
};H1290. Word Pattern
Given a pattern and a string s, find if s follows the same pattern.
Here follow means a full match, such that there is a bijection between a letter in pattern and a non-empty word in s.
Example 1:
plaintext
Input: pattern = "abba", s = "dog cat cat dog"
Output: trueExample 2:
plaintext
Input: pattern = "abba", s = "dog cat cat fish"
Output: falseSolution:
js
/**
* @param {string} pattern
* @param {string} s
* @return {boolean}
*/
var wordPattern = function (pattern, s) {
// const str = s.split(" "), map = new Map(), set = new Set();
// if (pattern.length !== str.length) return false;
// for (let i = 0; i < str.length; i++) {
// if ((map.has(pattern[i]) && str[i] !== map.get(pattern[i])) || (!map.has(pattern[i]) && set.has(str[i]))) {
// return false;
// } else {
// map.set(pattern[i], str[i]);
// set.add(str[i]);
// }
// }
// return true;
const str = s.split(" ");
if (pattern.length !== str.length) return false;
for (let i = 0; i < str.length; i++) {
if (str.indexOf(str[i]) !== pattern.indexOf(pattern[i])) return false;
}
return true;
};H1322. Coin Change
You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.
Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
You may assume that you have an infinite number of each kind of coin.
Example 1:
plaintext
Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1Solution:
js
/**
* @param {number[]} coins
* @param {number} amount
* @return {number}
*/
var coinChange = function (coins, amount) {
const dp = Array(amount + 1).fill(Infinity);
dp[0] = 0;
for (let i = 1; i < amount + 1; i++) {
for (const c of coins) {
if (i >= c) dp[i] = Math.min(dp[i], dp[i - c] + 1);
}
}
return dp[amount] === Infinity ? -1 : dp[amount];
};H1328. Odd Even Linked List
Given the head of a singly linked list, group all the nodes with odd indices together followed by the nodes with even indices, and return the reordered list.
The first node is considered odd, and the second node is even, and so on.
Note that the relative order inside both the even and odd groups should remain as it was in the input.
You must solve the problem in O(1) extra space complexity and O(n) time complexity.
Example 1:
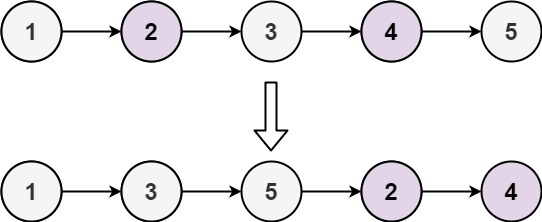
plaintext
Input: head = [1,2,3,4,5]
Output: [1,3,5,2,4]Solution:
js
/**
* Definition for singly-linked list.
* function ListNode(val, next) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
*/
/**
* @param {ListNode} head
* @return {ListNode}
*/
var oddEvenList = function(head) {
if (!head) return head;
let even = head.next, odd = head;
while (odd.next && odd.next.next) {
let temp = odd.next;
odd.next = odd.next.next;
odd = odd.next;
temp.next = odd.next;
}
odd.next = even;
return head;
};H1334. Increasing Triplet Subsequence
Given an integer array nums, return true if there exists a triple of indices (i, j, k) such that i < j < k and nums[i] < nums[j] < nums[k]. If no such indices exists, return false.
Example 1:
plaintext
Input: nums = [1,2,3,4,5]
Output: true
Explanation: Any triplet where i < j < k is valid.Example 2:
plaintext
Input: nums = [5,4,3,2,1]
Output: false
Explanation: No triplet exists.Solution:
js
/**
* @param {number[]} nums
* @return {boolean}
*/
var increasingTriplet = function (nums) {
let a = b = Infinity;
for (let i = 0; i < nums.length; i++) {
if (a >= nums[i]) {
a = nums[i];
} else if (b >= nums[i]) {
b = nums[i];
} else {
return true;
}
}
return false;
};H1394. Decode String
Given an encoded string, return its decoded string.
The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. Note that k is guaranteed to be a positive integer.
You may assume that the input string is always valid; there are no extra white spaces, square brackets are well-formed, etc. Furthermore, you may assume that the original data does not contain any digits and that digits are only for those repeat numbers, k. For example, there will not be input like 3a or 2[4].
The test cases are generated so that the length of the output will never exceed 105.
Example 1:
plaintext
Input: s = "3[a]2[bc]"
Output: "aaabcbc"Example 2:
plaintext
Input: s = "3[a2[c]]"
Output: "accaccacc"Solution:
js
/**
* @param {string} s
* @return {string}
*/
var decodeString = function (s) {
const stack = [];
for (const str of s) {
if (str !== "]") { stack.push(str); continue; }
let curr = stack.pop(), strs = "";
while (curr !== "[") {
strs = curr + strs;
curr = stack.pop();
}
curr = stack.pop();
let count = "";
while (!isNaN(curr)) {
count = curr + count;
curr = stack.pop();
}
if (curr) stack.push(curr);
stack.push(strs.repeat(Number(count)));
}
return stack.join("");
};H1399. Evaluate Division
You are given an array of variable pairs equations and an array of real numbers values, where equations[i] = [Ai, Bi] and values[i] represent the equation Ai / Bi = values[i]. Each Ai or Bi is a string that represents a single variable.
You are also given some queries, where queries[j] = [Cj, Dj] represents the jth query where you must find the answer for Cj / Dj = ?.
Return the answers to all queries. If a single answer cannot be determined, return -1.0.
Note: The input is always valid. You may assume that evaluating the queries will not result in division by zero and that there is no contradiction.
Note: The variables that do not occur in the list of equations are undefined, so the answer cannot be determined for them.
Example 1:
plaintext
Input: equations = [["a","b"],["b","c"]], values = [2.0,3.0], queries = [["a","c"],["b","a"],["a","e"],["a","a"],["x","x"]]
Output: [6.00000,0.50000,-1.00000,1.00000,-1.00000]
Explanation:
Given: a / b = 2.0, b / c = 3.0
queries are: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
return: [6.0, 0.5, -1.0, 1.0, -1.0 ]
note: x is undefined => -1.0Solution:
js
/**
* @param {string[][]} equations
* @param {number[]} values
* @param {string[][]} queries
* @return {number[]}
*/
var calcEquation = function (equations, values, queries) {
const adj = new Map();
equations.forEach(([s, e], i) => {
if (!adj.has(s)) adj.set(s, new Map());
adj.get(s).set(e, values[i]);
if (!adj.has(e)) adj.set(e, new Map());
adj.get(e).set(s, 1 / values[i]);
});
const dfs = (s, e, vis = new Set()) => {
if (!adj.has(s) || !adj.has(e)) return -1;
vis.add(s);
if (s === e) return 1;
for (const [u, v] of [...adj.get(s)]) {
if (!vis.has(u)) {
const div = dfs(u, e, vis);
if (div !== -1) return div * v;
}
}
return -1;
}
return queries.map(([s, e]) => dfs(s, e));
};H1443. String Compression
Given an array of characters chars, compress it using the following algorithm:
Begin with an empty string s. For each group of consecutive repeating characters in chars:
- If the group's length is
1, append the character tos. - Otherwise, append the character followed by the group's length.
The compressed string s should not be returned separately, but instead, be stored in the input character array chars. Note that group lengths that are 10 or longer will be split into multiple characters in chars.
After you are done modifying the input array, return the new length of the array.
You must write an algorithm that uses only constant extra space.
Example 1:
plaintext
Input: chars = ["a","a","b","b","c","c","c"]
Output: Return 6, and the first 6 characters of the input array should be: ["a","2","b","2","c","3"]
Explanation: The groups are "aa", "bb", and "ccc". This compresses to "a2b2c3".Example 2:
plaintext
Input: chars = ["a"]
Output: Return 1, and the first character of the input array should be: ["a"]
Explanation: The only group is "a", which remains uncompressed since it's a single character.Solution:
js
/**
* @param {character[]} chars
* @return {number}
*/
var compress = function (chars) {
let count = 1, index = 0;
for (let i = 1; i <= chars.length; i++) {
if (chars[i - 1] === chars[i]) {
count++;
} else {
chars[index++] = chars[i - 1];
if (count > 1) {
for (let j = 0; j < String(count).length; j++) {
chars[index++] = String(count)[j];
}
}
count = 1;
}
}
return index;
};H1450. Delete Node in a BST
Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.
Basically, the deletion can be divided into two stages:
- Search for a node to remove.
- If the node is found, delete the node.
Example 1:
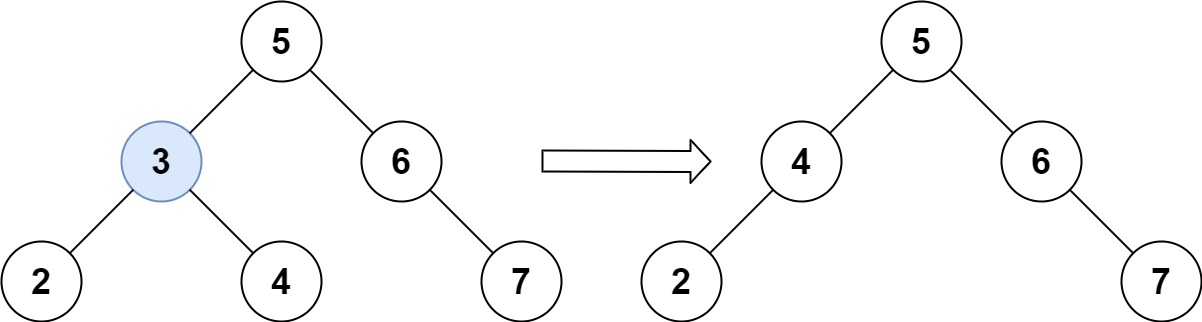
plaintext
Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} key
* @return {TreeNode}
*/
var deleteNode = function (root, key) {
const dfs = (node) => {
if (!node) return null;
if (node.val === key) {
if(!node.left) return node.right;
if(!node.right) return node.left;
let curr = node.right;
while(curr.left) curr = curr.left;
curr.left = node.left;
return node.right;
} else if (node.val > key) node.left = dfs(node.left);
else node.right = dfs(node.right);
return node;
}
return dfs(root);
};H1452. Minimum Number of Arrows to Burst Balloons
There are some spherical balloons taped onto a flat wall that represents the XY-plane. The balloons are represented as a 2D integer array points where points[i] = [xstart, xend] denotes a balloon whose horizontal diameter stretches between xstart and xend. You do not know the exact y-coordinates of the balloons.
Arrows can be shot up directly vertically (in the positive y-direction) from different points along the x-axis. A balloon with xstart and xend is burst by an arrow shot at x if xstart <= x <= xend. There is no limit to the number of arrows that can be shot. A shot arrow keeps traveling up infinitely, bursting any balloons in its path.
Given the array points, return the minimum number of arrows that must be shot to burst all balloons.
Example 1:
plaintext
Input: points = [[10,16],[2,8],[1,6],[7,12]]
Output: 2
Explanation: The balloons can be burst by 2 arrows:
- Shoot an arrow at x = 6, bursting the balloons [2,8] and [1,6].
- Shoot an arrow at x = 11, bursting the balloons [10,16] and [7,12].Solution:
js
/**
* @param {number[][]} points
* @return {number}
*/
var findMinArrowShots = function (points) {
points.sort((a, b) => a[1] - b[1]);
let prevEnd = points.shift()[1], min = 1;
for (const point of points) {
if (prevEnd < point[0]) {
prevEnd = point[1];
min++;
}
}
return min;
};Note: 为什么是右端点排序,是因为你试想,箭射的是两个气球间的重叠部分,对于第一个气球来说,贪心选择是射它最右边的端点能保证尽可能一箭多球,所以所有的气球应该按照右端点排序。
H1530. Minimum Absolute Difference in BST
Given the root of a Binary Search Tree (BST), return the minimum absolute difference between the values of any two different nodes in the tree.
Example 1:
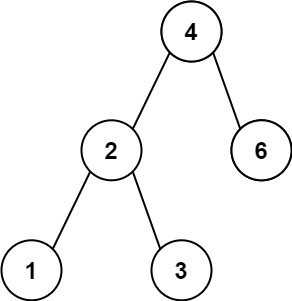
plaintext
Input: root = [4,2,6,1,3]
Output: 1Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var getMinimumDifference = function (root) {
const arr = [];
let min = 1e5;
const dfs = (node) => {
if (!node) return;
dfs(node.left);
arr.push(node.val);
dfs(node.right);
}
dfs(root);
for (let i = 1; i < arr.length; i++) {
min = Math.min(min, arr[i] - arr[i - 1]);
}
return min;
};H1559. Maximum Depth of N-ary Tree
Given a n-ary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).
Example 1:
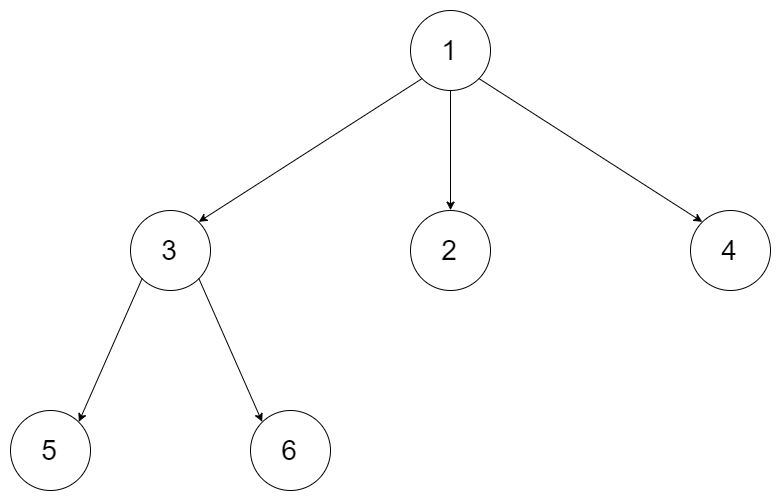
plaintext
Input: root = [1,null,3,2,4,null,5,6]
Output: 3Solution:
js
/**
* @param {Node|null} root
* @return {number}
*/
var maxDepth = function(root) {
if(!root) return 0
let depth = 0
for (let child of root.children) {
depth = Math.max(depth, maxDepth(child))
}
return depth+1
};H1590. N-ary Tree Postorder Traversal
Given the root of an n-ary tree, return the postorder traversal of its nodes' values.
Nary-Tree input serialization is represented in their level order traversal. Each group of children is separated by the null value (See examples)
Example 1:

plaintext
Input: root = [1,null,3,2,4,null,5,6]
Output: [5,6,3,2,4,1]Solution:
js
/**
* // Definition for a Node.
* function Node(val,children) {
* this.val = val;
* this.children = children;
* };
*/
/**
* @param {Node|null} root
* @return {number[]}
*/
var postorder = function(root) {
let res = [];
const dfs = (node) => {
if (!node) return;
for (const n of node.children) dfs(n);
res.push(node.val);
}
dfs(root);
return res;
};H1617. Merge Two Binary Trees
You are given two binary trees root1 and root2.
Imagine that when you put one of them to cover the other, some nodes of the two trees are overlapped while the others are not. You need to merge the two trees into a new binary tree. The merge rule is that if two nodes overlap, then sum node values up as the new value of the merged node. Otherwise, the NOT null node will be used as the node of the new tree.
Return the merged tree.
Note: The merging process must start from the root nodes of both trees.
Example 1:

plaintext
Input: root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
Output: [3,4,5,5,4,null,7]Solution:
js
var mergeTrees = function (root1, root2) {
if (!root1) return root2;
if (!root2) return root1;
root1.val += root2.val;
root1.left = mergeTrees(root1.left, root2.left);
root1.right = mergeTrees(root1.right, root2.right);
return root1;
};H1637. Average of Levels in Binary Tree
Given the root of a binary tree, return the average value of the nodes on each level in the form of an array. Answers within 10-5 of the actual answer will be accepted.
Example 1:
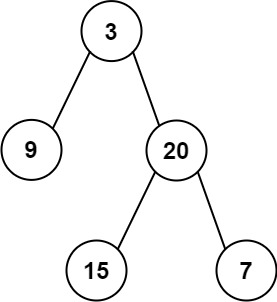
plaintext
Input: root = [3,9,20,null,null,15,7]
Output: [3.00000,14.50000,11.00000]
Explanation: The average value of nodes on level 0 is 3, on level 1 is 14.5, and on level 2 is 11.
Hence return [3, 14.5, 11].Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number[]}
*/
var averageOfLevels = function (root) {
const res = [], queue = [root];
while (queue.length) {
let sum = 0;
const len = queue.length;
for (let i = 0; i < len; i++) {
const node = queue.shift();
sum += node.val;
if (node.left) queue.push(node.left);
if (node.right) queue.push(node.right);
}
res.push(sum / len);
}
return res;
};H1649. Dota2 Senate
In the world of Dota2, there are two parties: the Radiant and the Dire.
The Dota2 senate consists of senators coming from two parties. Now the Senate wants to decide on a change in the Dota2 game. The voting for this change is a round-based procedure. In each round, each senator can exercise one of the two rights:
- Ban one senator's right: A senator can make another senator lose all his rights in this and all the following rounds.
- Announce the victory: If this senator found the senators who still have rights to vote are all from the same party, he can announce the victory and decide on the change in the game.
Given a string senate representing each senator's party belonging. The character 'R' and 'D' represent the Radiant party and the Dire party. Then if there are n senators, the size of the given string will be n.
The round-based procedure starts from the first senator to the last senator in the given order. This procedure will last until the end of voting. All the senators who have lost their rights will be skipped during the procedure.
Suppose every senator is smart enough and will play the best strategy for his own party. Predict which party will finally announce the victory and change the Dota2 game. The output should be "Radiant" or "Dire".
Example 1:
plaintext
Input: senate = "RDD"
Output: "Dire"
Explanation:
The first senator comes from Radiant and he can just ban the next senator's right in round 1.
And the second senator can't exercise any rights anymore since his right has been banned.
And the third senator comes from Dire and he can ban the first senator's right in round 1.
And in round 2, the third senator can just announce the victory since he is the only guy in the senate who can vote.Solution:
js
/**
* @param {string} senate
* @return {string}
*/
var predictPartyVictory = function(senate) {
const d = [], r = [], len = senate.length;
for (let i = 0; i < len; i++) {
if (senate[i] === "R") r.push(i);
else d.push(i);
}
while (d.length && r.length) {
const d1 = d.shift(), r1 = r.shift();
if (d1 < r1) d.push(d1 + len);
else r.push(r1 + len);
}
return d.length ? "Dire" : "Radiant";
};H1735. Asteroid Collision
We are given an array asteroids of integers representing asteroids in a row.
For each asteroid, the absolute value represents its size, and the sign represents its direction (positive meaning right, negative meaning left). Each asteroid moves at the same speed.
Find out the state of the asteroids after all collisions. If two asteroids meet, the smaller one will explode. If both are the same size, both will explode. Two asteroids moving in the same direction will never meet.
Example 1:
plaintext
Input: asteroids = [5,10,-5]
Output: [5,10]
Explanation: The 10 and -5 collide resulting in 10. The 5 and 10 never collide.Solution:
js
/**
* @param {number[]} asteroids
* @return {number[]}
*/
var asteroidCollision = function (asteroids) {
const stack = [asteroids[0]];
for (let i = 1; i < asteroids.length; i++) {
let l = stack.at(-1), r = asteroids[i];
if (l > 0 && r < 0) {
while (stack.at(-1) > 0 && r < 0) {
if (stack.at(-1) < -r) {
stack.pop();
} else if (stack.at(-1) === -r) {
stack.pop();
r = 0;
} else {
r = 0;
}
}
if (r < 0) stack.push(r);
} else {
stack.push(r);
}
}
return stack;
};H1746. Min Cost Climbing Stairs
You are given an integer array cost where cost[i] is the cost of ith step on a staircase. Once you pay the cost, you can either climb one or two steps.
You can either start from the step with index 0, or the step with index 1.
Return the minimum cost to reach the top of the floor.
Example 1:
plaintext
Input: cost = [10,15,20]
Output: 15
Explanation: You will start at index 1.
- Pay 15 and climb two steps to reach the top.
The total cost is 15.Solution:
js
/**
* @param {number[]} cost
* @return {number}
*/
var minCostClimbingStairs = function (cost) {
let len = cost.length - 1;
const dp = [];
while (len >= 0) {
dp[len] = cost[len] + Math.min(dp[len + 1] || 0, dp[len + 2] || 0);
len--;
}
return Math.min(dp[0], dp[1]);
};Hint:
- Build an array dp where dp[i] is the minimum cost to climb to the top starting from the ith staircase.
- Assuming we have n staircase labeled from 0 to n - 1 and assuming the top is n, then dp[n] = 0, marking that if you are at the top, the cost is 0.
- Now, looping from n - 1 to 0, the dp[i] = cost[i] + min(dp[i + 1], dp[i + 2]). The answer will be the minimum of dp[0] and dp[1]
H1807. Max Increase to Keep City Skyline
There is a city composed of n x n blocks, where each block contains a single building shaped like a vertical square prism. You are given a 0-indexed n x n integer matrix grid where grid[r][c] represents the height of the building located in the block at row r and column c.
A city's skyline is the outer contour formed by all the building when viewing the side of the city from a distance. The skyline from each cardinal direction north, east, south, and west may be different.
We are allowed to increase the height of any number of buildings by any amount (the amount can be different per building). The height of a 0-height building can also be increased. However, increasing the height of a building should not affect the city's skyline from any cardinal direction.
Return the maximum total sum that the height of the buildings can be increased by without changing the city's skyline from any cardinal direction.
Example 1:
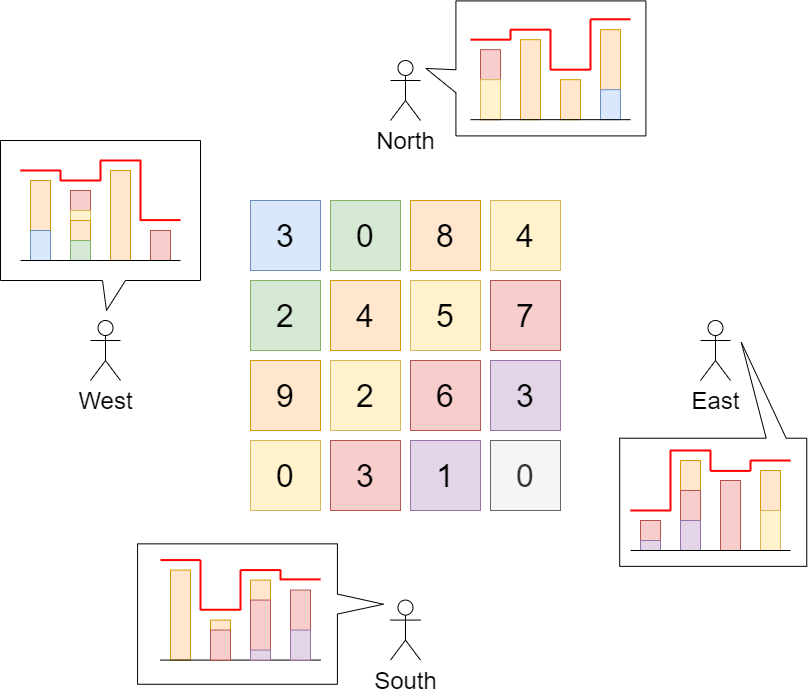
plaintext
Input: grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
Output: 35
Explanation: The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = [ [8, 4, 8, 7],
[7, 4, 7, 7],
[9, 4, 8, 7],
[3, 3, 3, 3] ]Solution:
js
/**
* @param {number[][]} grid
* @return {number}
*/
var maxIncreaseKeepingSkyline = function (grid) {
let res = 0, len = grid.length, max_col = [], max_row = [];
for (let i = 0; i < len; i++) {
max_row.push(Math.max(...grid[i]));
for (let j = 0; j < len; j++) {
max_col[j] = max_col[j] > -1 ? Math.max(max_col[j], grid[i][j]) : grid[i][j];
}
}
for (let i = 0; i < len; i++) {
for (let j = 0; j < len; j++) {
const min = Math.min(max_row[i], max_col[j]);
if (grid[i][j] < min) res += min - grid[i][j];
}
}
return res;
};H1841. Keys and Rooms
There are n rooms labeled from 0 to n - 1 and all the rooms are locked except for room 0. Your goal is to visit all the rooms. However, you cannot enter a locked room without having its key.
When you visit a room, you may find a set of distinct keys in it. Each key has a number on it, denoting which room it unlocks, and you can take all of them with you to unlock the other rooms.
Given an array rooms where rooms[i] is the set of keys that you can obtain if you visited room i, return true if you can visit all the rooms, or false otherwise.
Example 1:
plaintext
Input: rooms = [[1],[2],[3],[]]
Output: true
Explanation:
We visit room 0 and pick up key 1.
We then visit room 1 and pick up key 2.
We then visit room 2 and pick up key 3.
We then visit room 3.
Since we were able to visit every room, we return true.Solution:
js
/**
* @param {number[][]} rooms
* @return {boolean}
*/
var canVisitAllRooms = function (rooms) {
const v = new Set([0]), q = [0];
while (q.length) {
const crt = q.shift();
for (const k of rooms[crt]) {
if (!v.has(k)) {
q.push(k);
v.add(k);
}
}
}
return v.size === rooms.length;
};H1872. Leaf-Similar Trees
Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a leaf value sequence*.*
For example, in the given tree above, the leaf value sequence is (6, 7, 4, 9, 8).
Two binary trees are considered leaf-similar if their leaf value sequence is the same.
Return true if and only if the two given trees with head nodes root1 and root2 are leaf-similar.
Example 1:
plaintext
Input: root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8]
Output: trueSolution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root1
* @param {TreeNode} root2
* @return {boolean}
*/
var leafSimilar = function (root1, root2) {
const dfs = (node) => {
if (!node) return [];
const leaves = [...dfs(node.left), ...dfs(node.right)];
return leaves.length > 0 ? leaves : [node.val];
}
return JSON.stringify(dfs(root1)) === JSON.stringify(dfs(root2));
}H1897. Increasing Order Search Tree
Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.
Example 1:
plaintext
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var increasingBST = function(root) {
let newRoot = newTree = null;
const dfs = (node) => {
if (!node) return;
dfs(node.left);
if (!newRoot) {
newRoot = newTree = node;
} else {
newTree.right = node;
newTree = newTree.right;
newTree.left = null;
}
dfs(node.right);
}
dfs(root);
return newRoot;
};H1933. Number of Recent Calls
You have a RecentCounter class which counts the number of recent requests within a certain time frame.
Implement the RecentCounter class:
RecentCounter()Initializes the counter with zero recent requests.int ping(int t)Adds a new request at timet, wheretrepresents some time in milliseconds, and returns the number of requests that has happened in the past3000milliseconds (including the new request). Specifically, return the number of requests that have happened in the inclusive range[t - 3000, t].
It is guaranteed that every call to ping uses a strictly larger value of t than the previous call.
Example 1:
plaintext
Input
["RecentCounter", "ping", "ping", "ping", "ping"]
[[], [1], [100], [3001], [3002]]
Output
[null, 1, 2, 3, 3]
Explanation
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = [1], range is [-2999,1], return 1
recentCounter.ping(100); // requests = [1, 100], range is [-2900,100], return 2
recentCounter.ping(3001); // requests = [1, 100, 3001], range is [1,3001], return 3
recentCounter.ping(3002); // requests = [1, 100, 3001, 3002], range is [2,3002], return 3Solution:
js
var RecentCounter = function () {
this.queue = [];
};
/**
* @param {number} t
* @return {number}
*/
RecentCounter.prototype.ping = function (t) {
while (this.queue.length !== 0 && this.queue[0] < t - 3000) {
this.queue.shift();
}
this.queue.push(t);
return this.queue.length;
};
/**
* Your RecentCounter object will be instantiated and called as such:
* var obj = new RecentCounter()
* var param_1 = obj.ping(t)
*/Note:
- I suddenly found we can write more than one condition in
whileloop.
H1938. Range Sum of BST
Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].
Example 1:
plaintext
Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
Output: 32
Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} low
* @param {number} high
* @return {number}
*/
var rangeSumBST = function (root, low, high) {
let sum = 0;
const dfs = (node) => {
if (!node) return;
if (low <= node.val && node.val <= high) sum += node.val;
if (node.val < low || node.val < high) dfs(node.right);
if (node.val > high || node.val > low) dfs(node.left);
}
dfs(root);
return sum;
};H1997. Find the Town Judge
In a town, there are n people labeled from 1 to n. There is a rumor that one of these people is secretly the town judge.
If the town judge exists, then:
- The town judge trusts nobody.
- Everybody (except for the town judge) trusts the town judge.
- There is exactly one person that satisfies properties 1 and 2.
You are given an array trust where trust[i] = [ai, bi] representing that the person labeled ai trusts the person labeled bi. If a trust relationship does not exist in trust array, then such a trust relationship does not exist.
Return the label of the town judge if the town judge exists and can be identified, or return -1 otherwise.
Example 1:
plaintext
Input: n = 3, trust = [[1,3],[2,3]]
Output: 3Example 2:
plaintext
Input: n = 3, trust = [[1,3],[2,3],[3,1]]
Output: -1Solution:
js
/**
* @param {number} n
* @param {number[][]} trust
* @return {number}
*/
var findJudge = function (n, trust) {
const adj = Array.from({ length: n + 1 }, () => []);
for (const t of trust) adj[t[0]].push(t[1]);
const judge = adj.findLastIndex(item => !item.length);
if (judge > 0) {
const isTrustedByEveryone = adj.every((item, i) => {
if (i === judge || i === 0) return true;
return item.includes(judge);
});
if (isTrustedByEveryone) return judge;
}
return -1;
};H11004. Max Consecutive Ones III
Given a binary array nums and an integer k, return the maximum number of consecutive 1's in the array if you can flip at most k 0's.
Example 1:
plaintext
Input: nums = [1,1,1,0,0,0,1,1,1,1,0], k = 2
Output: 6
Explanation: [1,1,1,0,0,1,1,1,1,1,1]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.Solution:
js
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var longestOnes = function (nums, k) {
let i = j = max = zeros = 0;
while (j < nums.length) {
if (nums[j]) {
j++;
} else if (zeros < k) {
j++;
zeros++;
} else {
if (!nums[i]) zeros--;
i++;
}
max = Math.max(max, j - i);
}
return max;
};H11021. Remove Outermost Parentheses
A valid parentheses string is either empty "", "(" + A + ")", or A + B, where A and B are valid parentheses strings, and + represents string concatenation.
- For example,
"","()","(())()", and"(()(()))"are all valid parentheses strings.
A valid parentheses string s is primitive if it is nonempty, and there does not exist a way to split it into s = A + B, with A and B nonempty valid parentheses strings.
Given a valid parentheses string s, consider its primitive decomposition: s = P1 + P2 + ... + Pk, where Pi are primitive valid parentheses strings.
Return s after removing the outermost parentheses of every primitive string in the primitive decomposition of s.
Example 1:
plaintext
Input: s = "(()())(())"
Output: "()()()"
Explanation:
The input string is "(()())(())", with primitive decomposition "(()())" + "(())".
After removing outer parentheses of each part, this is "()()" + "()" = "()()()".Solution:
js
/**
* @param {string} s
* @return {string}
*/
var removeOuterParentheses = function (s) {
let stack = 0;
let result = "";
for (const str of s) {
if (str === "(") {
if (stack) result += str;
stack++;
} else {
stack--;
if (stack) result += str;
}
}
return result;
};Note:
- Use
constto declarestr.stackis not necessarily to be[], because we don't need to use value of this array. So we might as well use Number to check if each part comes to an end.
H11207. Unique Number of Occurrences
Given an array of integers arr, return true if the number of occurrences of each value in the array is unique or false otherwise.
Example 1:
plaintext
Input: arr = [1,2,2,1,1,3]
Output: true
Explanation: The value 1 has 3 occurrences, 2 has 2 and 3 has 1. No two values have the same number of occurrences.Example 2:
plaintext
Input: arr = [1,2]
Output: falseSolution:
js
/**
* @param {number[]} arr
* @return {boolean}
*/
var uniqueOccurrences = function (arr) {
const hash = {};
arr.forEach((a) => {
hash[a] = (hash[a] || 0) + 1;
})
const vals = Object.values(hash);
const set = new Set(vals)
return vals.length === set.size;
};H11221. Split a String in Balanced Strings
Balanced strings are those that have an equal quantity of 'L' and 'R' characters.
Given a balanced string s, split it into some number of substrings such that:
- Each substring is balanced.
Return the maximum number of balanced strings you can obtain.
Example 1:
plaintext
Input: s = "RLRRLLRLRL"
Output: 4
Explanation: s can be split into "RL", "RRLL", "RL", "RL", each substring contains same number of 'L' and 'R'.Solution:
js
/**
* @param {string} s
* @return {number}
*/
var balancedStringSplit = function (s) {
let count = stack = 0;
for (const str of s) {
stack += str === "L" ? 1 : -1;
if (!stack) count++;
}
return count;
};H11282. Group the People Given the Group Size They Belong To
There are n people that are split into some unknown number of groups. Each person is labeled with a unique ID from 0 to n - 1.
You are given an integer array groupSizes, where groupSizes[i] is the size of the group that person i is in. For example, if groupSizes[1] = 3, then person 1 must be in a group of size 3.
Return a list of groups such that each person i is in a group of size groupSizes[i].
Each person should appear in exactly one group, and every person must be in a group. If there are multiple answers, return any of them. It is guaranteed that there will be at least one valid solution for the given input.
Example 1:
plaintext
Input: groupSizes = [3,3,3,3,3,1,3]
Output: [[5],[0,1,2],[3,4,6]]
Explanation:
The first group is [5]. The size is 1, and groupSizes[5] = 1.
The second group is [0,1,2]. The size is 3, and groupSizes[0] = groupSizes[1] = groupSizes[2] = 3.
The third group is [3,4,6]. The size is 3, and groupSizes[3] = groupSizes[4] = groupSizes[6] = 3.
Other possible solutions are [[2,1,6],[5],[0,4,3]] and [[5],[0,6,2],[4,3,1]].Example 2:
plaintext
Input: groupSizes = [2,1,3,3,3,2]
Output: [[1],[0,5],[2,3,4]]Solution:
js
/**
* @param {number[]} groupSizes
* @return {number[][]}
*/
var groupThePeople = function (groupSizes) {
const hash = {}, result = [];
groupSizes.forEach((s, i) => {
hash[s] ||= [];
hash[s].push(i);
if (hash[s].length === s) {
result.push(hash[s]);
hash[s] = [];
}
})
return result;
};Note: It took me 40 minutes to figure it out.
ifstatement here is the point.
H11379. Find a Corresponding Node of a Binary Tree in a Clone of That Tree
Given two binary trees original and cloned and given a reference to a node target in the original tree.
The cloned tree is a copy of the original tree.
Return a reference to the same node in the cloned tree.
Note that you are not allowed to change any of the two trees or the target node and the answer must be a reference to a node in the cloned tree.
Example 1:
plaintext
Input: tree = [7,4,3,null,null,6,19], target = 3
Output: 3
Explanation: In all examples the original and cloned trees are shown. The target node is a green node from the original tree. The answer is the yellow node from the cloned tree.Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val) {
* this.val = val;
* this.left = this.right = null;
* }
*/
/**
* @param {TreeNode} original
* @param {TreeNode} cloned
* @param {TreeNode} target
* @return {TreeNode}
*/
var getTargetCopy = function (original, cloned, target) {
const dfs = (o, c) => {
if (!o) return;
if (o === target) return c;
return dfs(o.left, c.left) || dfs(o.right, c.right);
}
return dfs(original, cloned);
};H11402. Reducing Dishes
A chef has collected data on the satisfaction level of his n dishes. Chef can cook any dish in 1 unit of time.
Like-time coefficient of a dish is defined as the time taken to cook that dish including previous dishes multiplied by its satisfaction level i.e. time[i] * satisfaction[i].
Return the maximum sum of like-time coefficient that the chef can obtain after preparing some amount of dishes.
Dishes can be prepared in any order and the chef can discard some dishes to get this maximum value.
Example 1:
plaintext
Input: satisfaction = [-1,-8,0,5,-9]
Output: 14
Explanation: After Removing the second and last dish, the maximum total like-time coefficient will be equal to (-1*1 + 0*2 + 5*3 = 14).
Each dish is prepared in one unit of time.Solution:
js
/**
* @param {number[]} satisfaction
* @return {number}
*/
var maxSatisfaction = function (satisfaction) {
satisfaction.sort((a, b) => b - a);
let sum = max = 0;
for (const s of satisfaction) {
sum += s;
if (sum < 0) break;
max += sum;
}
return max;
};Note: If sum < 0, that means we don't need the rest of them anymore. Look, [-4, 5] and [5],which sum of like-time coefficient is bigger? Definitely the former one, so we should ensure sum is more than 0 to keep the maximum sum.
H11456. Maximum Number of Vowels in a Substring of Given Length
Given a string s and an integer k, return the maximum number of vowel letters in any substring of s with length k.
Vowel letters in English are 'a', 'e', 'i', 'o', and 'u'.
Example 1:
plaintext
Input: s = "abciiidef", k = 3
Output: 3
Explanation: The substring "iii" contains 3 vowel letters.Solution:
js
/**
* @param {string} s
* @param {number} k
* @return {number}
*/
var maxVowels = function (s, k) {
const vowels = new Set(["a","e","i","o","u"]);
let curr = "", max = crt = 0;
for (let i = 0; i < k; i++) if (vowels.has(s[i])) max++;
crt = max;
for (let i = 0, j = k; j < s.length; i++, j++) {
if (vowels.has(s[i])) crt--;
if (vowels.has(s[j])) crt++;
max = Math.max(max, crt);
}
return max;
};H11493. Longest Subarray of 1's After Deleting One Element
Given a binary array nums, you should delete one element from it.
Return the size of the longest non-empty subarray containing only 1's in the resulting array. Return 0 if there is no such subarray.
Example 1:
plaintext
Input: nums = [1,1,0,1]
Output: 3
Explanation: After deleting the number in position 2, [1,1,1] contains 3 numbers with value of 1's.Solution:
js
/**
* @param {number[]} nums
* @return {number}
*/
var longestSubarray = function(nums) {
let i = j = max = 0, hasZero = false;
while (j < nums.length) {
if (nums[j]) {
j++;
} else if (!hasZero) {
j++;
hasZero = true;
} else {
if (!nums[i]) hasZero = false;
i++;
}
max = Math.max(max, j - i);
}
return max - 1;
};H11512. Number of Good Pairs
Given an array of integers nums, return the number of good pairs.
A pair (i, j) is called good if nums[i] == nums[j] and i < j.
Example 1:
plaintext
Input: nums = [1,2,3,1,1,3]
Output: 4
Explanation: There are 4 good pairs (0,3), (0,4), (3,4), (2,5) 0-indexed.Example 2:
plaintext
Input: nums = [1,1,1,1]
Output: 6
Explanation: Each pair in the array are good.Solution:
js
/**
* @param {number[]} nums
* @return {number}
*/
var numIdenticalPairs = function (nums) {
const obj = {};
for (const n of nums) {
obj[n] = (obj[n] || 0) + 1;
}
return Object.entries(obj).reduce((acc, [_, val]) => {
if (val > 1) acc += (val - 1) * val / 2;
return acc;
}, 0)
};H11539. Kth Missing Positive Number
Given an array arr of positive integers sorted in a strictly increasing order, and an integer k.
Return the kth positive integer that is missing from this array.
Example 1:
plaintext
Input: arr = [2,3,4,7,11], k = 5
Output: 9
Explanation: The missing positive integers are [1,5,6,8,9,10,12,13,...]. The 5th missing positive integer is 9.Example 2:
plaintext
Input: arr = [1,2,3,4], k = 2
Output: 6
Explanation: The missing positive integers are [5,6,7,...]. The 2nd missing positive integer is 6.Solution:
js
/**
* @param {number[]} arr
* @param {number} k
* @return {number}
*/
var findKthPositive = function(arr, k) {
let i = 1;
let j = 0;
while(1) {
if (!arr.includes(i)) {
j++;
if (j == k) {
return i;
}
}
i++;
}
};H11615. Maximal Network Rank
There is an infrastructure of n cities with some number of roads connecting these cities. Each roads[i] = [ai, bi] indicates that there is a bidirectional road between cities ai and bi.
The network rank of two different cities is defined as the total number of directly connected roads to either city. If a road is directly connected to both cities, it is only counted once.
The maximal network rank of the infrastructure is the maximum network rank of all pairs of different cities.
Given the integer n and the array roads, return the maximal network rank of the entire infrastructure.
Example 1:
plaintext
Input: n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
Output: 4
Explanation: The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.Solution:
js
/**
* @param {number} n
* @param {number[][]} roads
* @return {number}
*/
var maximalNetworkRank = function (n, roads) {
let max = 0;
const adj = Array.from({length: n}, () => []);
for (let [a, b] of roads) {
adj[a].push(b);
adj[b].push(a);
}
for (let i = 0; i < n; i++) {
for (let j = i + 1; j < n; j++) {
let rank = adj[i].length + adj[j].length;
if (adj[i].includes(j)) rank--;
max = Math.max(max, rank);
}
}
return max;
};H11640. Check Array Formation Through Concatenation
You are given an array of distinct integers arr and an array of integer arrays pieces, where the integers in pieces are distinct. Your goal is to form arr by concatenating the arrays in pieces in any order. However, you are not allowed to reorder the integers in each array pieces[i].
Return true if it is possible to form the array arr from pieces. Otherwise, return false.
Example 1:
plaintext
Input: arr = [15,88], pieces = [[88],[15]]
Output: true
Explanation: Concatenate [15] then [88]Example 2:
plaintext
Input: arr = [49,18,16], pieces = [[16,18,49]]
Output: false
Explanation: Even though the numbers match, we cannot reorder pieces[0].Example 3:
plaintext
Input: arr = [91,4,64,78], pieces = [[78],[4,64],[91]]
Output: true
Explanation: Concatenate [91] then [4,64] then [78]Solution:
js
/**
* @param {number[]} arr
* @param {number[][]} pieces
* @return {boolean}
*/
var canFormArray = function (arr, pieces) {
const hash = {}, result = [];
pieces.forEach(piece => {
hash[piece[0]] = piece;
})
for (const a of arr) {
if (hash[a]) result.push(hash[a].flat());
}
return String(arr) === String(result);
};H11689. Partitioning Into Minimum Number Of Deci-Binary Numbers
A decimal number is called deci-binary if each of its digits is either 0 or 1 without any leading zeros. For example, 101 and 1100 are deci-binary, while 112 and 3001 are not.
Given a string n that represents a positive decimal integer, return the minimum number of positive deci-binary numbers needed so that they sum up to n.
Example 1:
plaintext
Input: n = "32"
Output: 3
Explanation: 10 + 11 + 11 = 32Example 2:
plaintext
Input: n = "82734"
Output: 8Example 3:
plaintext
Input: n = "27346209830709182346"
Output: 9Solution:
js
/**
* @param {string} n
* @return {number}
*/
var minPartitions = function (n) {
// return Math.max(...n);
for (let i = 9; i > 0; i--) {
if (n.indexOf(i) !== -1) return i;
}
};Note: The greediness lies in finding the biggest digit in
nat first.
H11848. Minimum Distance to the Target Element
Given an integer array nums (0-indexed) and two integers target and start, find an index i such that nums[i] == target and abs(i - start) is minimized. Note that abs(x) is the absolute value of x.
Return abs(i - start).
It is guaranteed that target exists in nums.
Example 1:
plaintext
Input: nums = [1,2,3,4,5], target = 5, start = 3
Output: 1
Explanation: nums[4] = 5 is the only value equal to target, so the answer is abs(4 - 3) = 1.Example 2:
plaintext
Input: nums = [1], target = 1, start = 0
Output: 0
Explanation: nums[0] = 1 is the only value equal to target, so the answer is abs(0 - 0) = 0.Solution:
js
/**
* @param {number[]} nums
* @param {number} target
* @param {number} start
* @return {number}
*/
var getMinDistance = function(nums, target, start) {
let min = 10000;
for (let i = 0; i < start; i++) {
if (nums[i] === target) {
min = start - i;
}
}
for (let i = start; i < start + min; i++) {
if (nums[i] === target) {
return i - start;
}
}
return min;
};H11971. Find if Path Exists in Graph
There is a bi-directional graph with n vertices, where each vertex is labeled from 0 to n - 1 (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [ui, vi] denotes a bi-directional edge between vertex ui and vertex vi. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself.
You want to determine if there is a valid path that exists from vertex source to vertex destination.
Given edges and the integers n, source, and destination, return true if there is a valid path from source to destination, or false otherwise*.*
Example 1:
plaintext
Input: n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
Output: false
Explanation: There is no path from vertex 0 to vertex 5.Solution:
js
/**
* @param {number} n
* @param {number[][]} edges
* @param {number} source
* @param {number} destination
* @return {boolean}
*/
var validPath = function(n, edges, source, destination) {
if (n === 1) return true;
const v = new Array(n).fill(0);
v[source] = 1;
let flag = true;
while (flag) {
flag = false;
for (const e of edges) {
if (v[e[0]] !== v[e[1]]) v[e[0]] = v[e[1]] = 1, flag = true;
if (v[destination]) return true;
}
}
return false;
};H12006. Count Number of Pairs With Absolute Difference K
Given an integer array nums and an integer k, return the number of pairs (i, j) where i < j such that |nums[i] - nums[j]| == k.
The value of |x| is defined as:
xifx >= 0.-xifx < 0.
Example 1:
plaintext
Input: nums = [1,2,2,1], k = 1
Output: 4Example 2:
plaintext
Input: nums = [1,3], k = 3
Output: 0
Explanation: There are no pairs with an absolute difference of 3.Solution:
js
/**
* @param {number[]} nums
* @param {number} k
* @return {number}
*/
var countKDifference = function (nums, k) {
let count = 0;
// for (let i = 0; i < nums.length; i++) {
// for (let j = i + 1; j < nums.length; j++) {
// if (Math.abs(nums[i] - nums[j]) === k) count++;
// }
// }
const hash = {};
for (const n of nums) {
hash[n] = (hash[n] || 0) + 1;
}
for (const n of nums) {
count += hash[n + k] || 0;
}
return count;
};H12224. Minimum Number of Operations to Convert Time
You are given two strings current and correct representing two 24-hour times.
24-hour times are formatted as "HH:MM", where HH is between 00 and 23, and MM is between 00 and 59. The earliest 24-hour time is 00:00, and the latest is 23:59.
In one operation you can increase the time current by 1, 5, 15, or 60 minutes. You can perform this operation any number of times.
Return the minimum number of operations needed to convert current to correct.
Example 1:
plaintext
Input: current = "02:30", correct = "04:35"
Output: 3
Explanation:
We can convert current to correct in 3 operations as follows:
- Add 60 minutes to current. current becomes "03:30".
- Add 60 minutes to current. current becomes "04:30".
- Add 5 minutes to current. current becomes "04:35".
It can be proven that it is not possible to convert current to correct in fewer than 3 operations.Solution:
js
/**
* @param {string} current
* @param {string} correct
* @return {number}
*/
var convertTime = function (current, correct) {
let diff = (Number(correct.slice(0, 2)) - Number(current.slice(0, 2))) * 60
+ Number(correct.slice(-2)) - Number(current.slice(-2));
let min = 0;
min += Math.floor(diff / 60);
diff %= 60;
min += Math.floor(diff / 15);
diff %= 15;
min += Math.floor(diff / 5);
diff %= 5;
min += diff;
return min;
};Note: You don't need to use
while, just calculate it.
H12265. Count Nodes Equal to Average of Subtree
Given the root of a binary tree, return the number of nodes where the value of the node is equal to the average of the values in its subtree.
Note:
- The average of
nelements is the sum of thenelements divided bynand rounded down to the nearest integer. - A subtree of
rootis a tree consisting ofrootand all of its descendants.
Example 1:
plaintext
Input: root = [4,8,5,0,1,null,6]
Output: 5
Explanation:
For the node with value 4: The average of its subtree is (4 + 8 + 5 + 0 + 1 + 6) / 6 = 24 / 6 = 4.
For the node with value 5: The average of its subtree is (5 + 6) / 2 = 11 / 2 = 5.
For the node with value 0: The average of its subtree is 0 / 1 = 0.
For the node with value 1: The average of its subtree is 1 / 1 = 1.
For the node with value 6: The average of its subtree is 6 / 1 = 6.Solution:
js
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {number}
*/
var averageOfSubtree = function (root) {
let count = 0;
const dfs = (node) => {
if (!node) return [0, 0];
const [leftSize, leftSum] = dfs(node.left);
const [rightSize, rightSum] = dfs(node.right);
const sum = node.val + leftSum + rightSum;
const size = 1 + leftSize + rightSize;
if (Math.floor(sum / size) === node.val) count++;
return [size, sum];
}
dfs(root);
return count;
};H12300. Successful Pairs of Spells and Potions
You are given two positive integer arrays spells and potions, of length n and m respectively, where spells[i] represents the strength of the ith spell and potions[j] represents the strength of the jth potion.
You are also given an integer success. A spell and potion pair is considered successful if the product of their strengths is at least success.
Return an integer array pairs of length n where pairs[i] is the number of potions that will form a successful pair with the ith spell.
Example 1:
plaintext
Input: spells = [5,1,3], potions = [1,2,3,4,5], success = 7
Output: [4,0,3]
Explanation:
- 0th spell: 5 * [1,2,3,4,5] = [5,10,15,20,25]. 4 pairs are successful.
- 1st spell: 1 * [1,2,3,4,5] = [1,2,3,4,5]. 0 pairs are successful.
- 2nd spell: 3 * [1,2,3,4,5] = [3,6,9,12,15]. 3 pairs are successful.
Thus, [4,0,3] is returned.Solution:
js
/**
* @param {number[]} spells
* @param {number[]} potions
* @param {number} success
* @return {number[]}
*/
var successfulPairs = function (spells, potions, success) {
potions.sort((a, b) => a - b);
const len = potions.length;
for (let i = 0; i < spells.length; i++) {
spells[i] = success / spells[i];
let l = 0, r = len - 1;
while (l <= r) {
const m = Math.floor((l + r) / 2);
if (potions[m] < spells[i]) {
l = m + 1;
} else {
r = m - 1;
}
}
spells[i] = len - l;
}
return spells;
};H12325. Decode the Message
You are given the strings key and message, which represent a cipher key and a secret message, respectively. The steps to decode message are as follows:
- Use the first appearance of all 26 lowercase English letters in
keyas the order of the substitution table. - Align the substitution table with the regular English alphabet.
- Each letter in
messageis then substituted using the table. - Spaces
' 'are transformed to themselves.
- For example, given
key = "**hap**p**y** **bo**y"(actual key would have at least one instance of each letter in the alphabet), we have the partial substitution table of ('h' -> 'a','a' -> 'b','p' -> 'c','y' -> 'd','b' -> 'e','o' -> 'f').
Return the decoded message.
Example 1:

plaintext
Input: key = "the quick brown fox jumps over the lazy dog", message = "vkbs bs t suepuv"
Output: "this is a secret"
Explanation: The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "the quick brown fox jumps over the lazy dog".Example 2:

plaintext
Input: key = "eljuxhpwnyrdgtqkviszcfmabo", message = "zwx hnfx lqantp mnoeius ycgk vcnjrdb"
Output: "the five boxing wizards jump quickly"
Explanation: The diagram above shows the substitution table.
It is obtained by taking the first appearance of each letter in "eljuxhpwnyrdgtqkviszcfmabo".Solution:
js
/**
* @param {string} key
* @param {string} message
* @return {string}
*/
var decodeMessage = function (key, message) {
const hash = {};
let result = "";
for (let i = j = 0; i < key.length; i++) {
if (key[i] !== " " && !hash[key[i]]) {
hash[key[i]] = String.fromCharCode("a".charCodeAt(0) + j);
if (j === 25) break;
j++;
}
}
for (const m of message) {
result += hash[m] || " ";
}
return result;
};H12352. Equal Row and Column Pairs
Given a 0-indexed n x n integer matrix grid, return the number of pairs (ri, cj) such that row ri and column cj are equal.
A row and column pair is considered equal if they contain the same elements in the same order (i.e., an equal array).
Example 1:
plaintext
Input: grid = [[3,1,2,2],[1,4,4,5],[2,4,2,2],[2,4,2,2]]
Output: 3
Explanation: There are 3 equal row and column pairs:
- (Row 0, Column 0): [3,1,2,2]
- (Row 2, Column 2): [2,4,2,2]
- (Row 3, Column 2): [2,4,2,2]Solution:
js
/**
* @param {number[][]} grid
* @return {number}
*/
var equalPairs = function (grid) {
const map = new Map();
let res = 0;
for (const arr of grid) {
const temp = arr.join("-") + "-";
map.set(temp, (map.get(temp) || 0) + 1);
}
for (let i = 0; i < grid.length; i++) {
let temp = "";
for (let j = 0; j < grid.length; j++) {
temp += grid[j][i] + "-";
}
if (map.has(temp)) res += map.get(temp);
}
return res;
};H12409. Count Days Spent Together
Alice and Bob are traveling to Rome for separate business meetings.
You are given 4 strings arriveAlice, leaveAlice, arriveBob, and leaveBob. Alice will be in the city from the dates arriveAlice to leaveAlice (inclusive), while Bob will be in the city from the dates arriveBob to leaveBob (inclusive). Each will be a 5-character string in the format "MM-DD", corresponding to the month and day of the date.
Return the total number of days that Alice and Bob are in Rome together.
You can assume that all dates occur in the same calendar year, which is not a leap year. Note that the number of days per month can be represented as: [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31].
Example 1:
plaintext
Input: arriveAlice = "08-15", leaveAlice = "08-18", arriveBob = "08-16", leaveBob = "08-19"
Output: 3
Explanation: Alice will be in Rome from August 15 to August 18. Bob will be in Rome from August 16 to August 19. They are both in Rome together on August 16th, 17th, and 18th, so the answer is 3.Solution:
js
/**
* @param {string} arriveAlice
* @param {string} leaveAlice
* @param {string} arriveBob
* @param {string} leaveBob
* @return {number}
*/
var countDaysTogether = function (arriveAlice, leaveAlice, arriveBob, leaveBob) {
if (arriveAlice > leaveBob || arriveBob > leaveAlice) return 0;
const dates = [arriveAlice, leaveAlice, arriveBob, leaveBob].sort();
const start = dates[1].split("-"), end = dates[2].split("-");
let sm = +start[0] - 1, em = +end[0] - 1, days = 0;
const sd = +start[1], ed = +end[1];
const months = [31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31];
while (sm < em) {
days += months[sm];
sm++;
}
return days - sd + ed + 1;
};H12824. Count Pairs Whose Sum is Less than Target
Given a 0-indexed integer array nums of length n and an integer target, return the number of pairs (i, j) where 0 <= i < j < n and nums[i] + nums[j] < target.
Example 1:
plaintext
Input: nums = [-1,1,2,3,1], target = 2
Output: 3
Explanation: There are 3 pairs of indices that satisfy the conditions in the statement:
- (0, 1) since 0 < 1 and nums[0] + nums[1] = 0 < target
- (0, 2) since 0 < 2 and nums[0] + nums[2] = 1 < target
- (0, 4) since 0 < 4 and nums[0] + nums[4] = 0 < target
Note that (0, 3) is not counted since nums[0] + nums[3] is not strictly less than the target.Solution:
js
/**
* @param {number[]} nums
* @param {number} target
* @return {number}
*/
var countPairs = function(nums, target) {
nums.sort((a, b) => a - b);
let l = 0, r = nums.length - 1, count = 0;
while (l < r) {
if (nums[l] + nums[r] < target) {
count += r - l;
l++;
} else {
r--;
}
}
return count;
};H12864. Maximum Odd Binary Number
You are given a binary string s that contains at least one '1'.
You have to rearrange the bits in such a way that the resulting binary number is the maximum odd binary number that can be created from this combination.
Return a string representing the maximum odd binary number that can be created from the given combination.
Note that the resulting string can have leading zeros.
Example 1:
plaintext
Input: s = "010"
Output: "001"
Explanation: Because there is just one '1', it must be in the last position. So the answer is "001".Solution:
js
/**
* @param {string} s
* @return {string}
*/
var maximumOddBinaryNumber = function (s) {
const arr = s.split("1");
const len = arr.length;
return "1".repeat(len - 2) + arr.join("") + "1";
};Note: The strategy is that we should put one
1at the end and the rest of them should come first.





