H1Basic Knowledege
H2Big O Notation
Big O notation is used to classify algorithms according to how their running time or space requirements grow as the input size grows.

| Big O Notation | Type | Computations for 10 elements | Computations for 100 elements | Computations for 1000 elements |
|---|---|---|---|---|
| O(1) | Constant | 1 | 1 | 1 |
| O(log N) | Logarithmic | 3 | 6 | 9 |
| O(N) | Linear | 10 | 100 | 1000 |
| O(N log N) | n log(n) | 30 | 600 | 9000 |
| O(N^2) | Quadratic | 100 | 10000 | 1000000 |
| O(2^N) | Exponential | 1024 | 1.26e+29 | 1.07e+301 |
| O(N!) | Factorial | 3628800 | 9.3e+157 | 4.02e+2567 |
H2Time Complexity
Time complexity measures the amount of time an algorithm takes to run as a function of the length of the input.
H2Space Complexity
Space complexity measures the amount of memory an algorithm uses as a function of the length of the input.
Below is the list of some of the most used Big O notations and their performance comparisons against different sizes of the input data.
H2Data Structure Operations Complexity
| Data Structure | Access | Search | Insertion | Deletion | Comments |
|---|---|---|---|---|---|
| Array | 1 | n | n | n | |
| Stack | n | n | 1 | 1 | |
| Queue | n | n | 1 | 1 | |
| Linked List | n | n | 1 | n | |
| Hash Table | - | n | n | n | In case of perfect hash function costs would be O(1) |
| Binary Search Tree | n | n | n | n | In case of balanced tree costs would be O(log(n)) |
| B-Tree | log(n) | log(n) | log(n) | log(n) | |
| Red-Black Tree | log(n) | log(n) | log(n) | log(n) | |
| AVL Tree | log(n) | log(n) | log(n) | log(n) | |
| Bloom Filter | - | 1 | 1 | - | False positives are possible while searching |
H2Array Sorting Algorithms Complexity
| Name | Best | Average | Worst | Memory | Stable | Comments |
|---|---|---|---|---|---|---|
| Bubble sort | n | n2 | n2 | 1 | Yes | |
| Insertion sort | n | n2 | n2 | 1 | Yes | |
| Selection sort | n2 | n2 | n2 | 1 | No | |
| Heap sort | n log(n) | n log(n) | n log(n) | 1 | No | |
| Merge sort | n log(n) | n log(n) | n log(n) | n | Yes | |
| Quick sort | n log(n) | n log(n) | n2 | log(n) | No | Quicksort is usually done in-place with O(log(n)) stack space |
| Shell sort | n log(n) | depends on gap sequence | n (log(n))2 | 1 | No | |
| Counting sort | n + r | n + r | n + r | n + r | Yes | r - biggest number in array |
| Radix sort | n * k | n * k | n * k | n + k | Yes | k - length of longest key |
H1Data Structures
H2Linked List

Note:
let a = head;In this scenario, if we runa.next = a.next.next, the linked list pointed to byheadwill change because we modified the property of a node.
H2Stack
LIFO (Last in, first out)
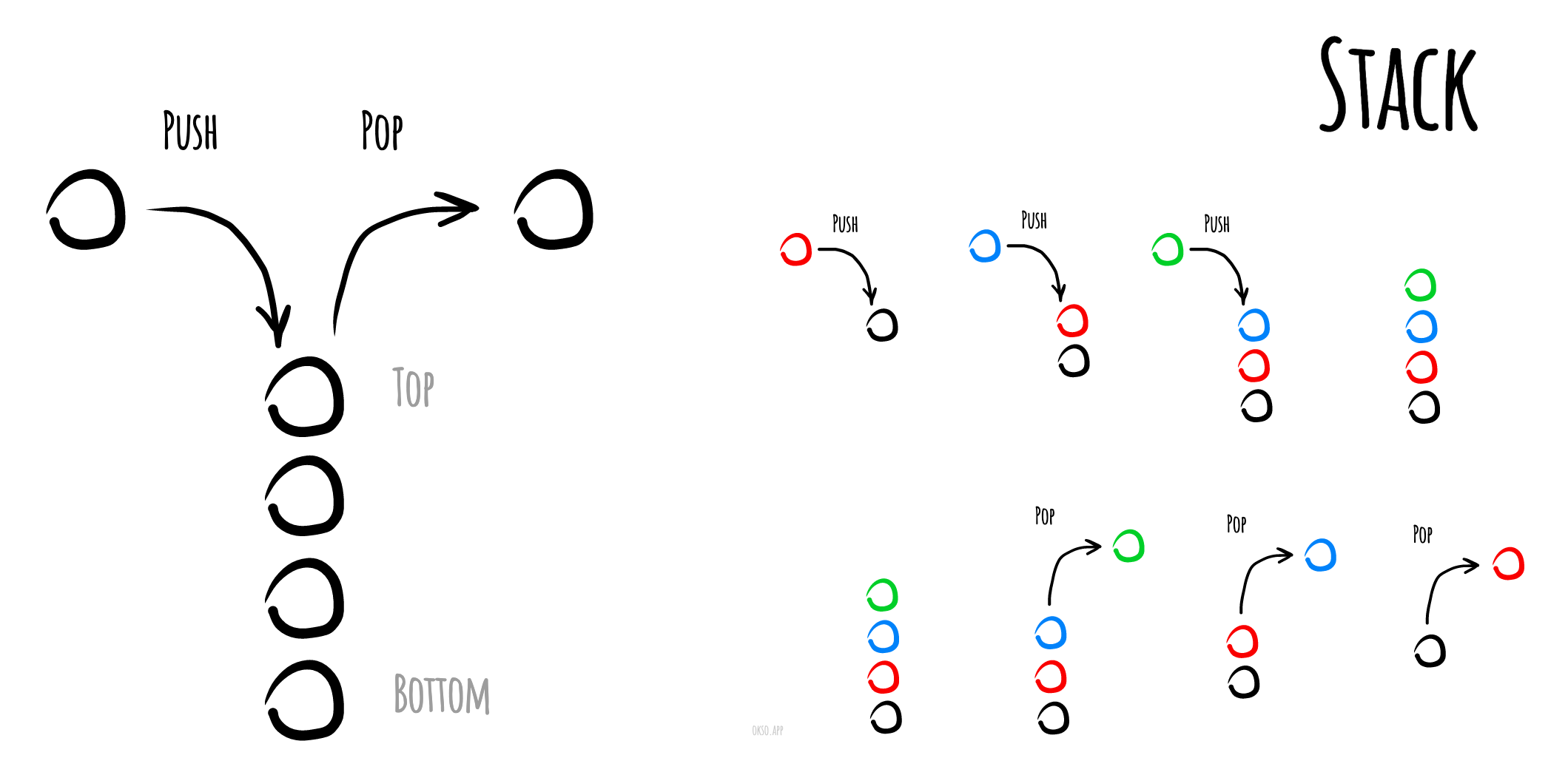
H2Queue
FIFO (First in, first out)
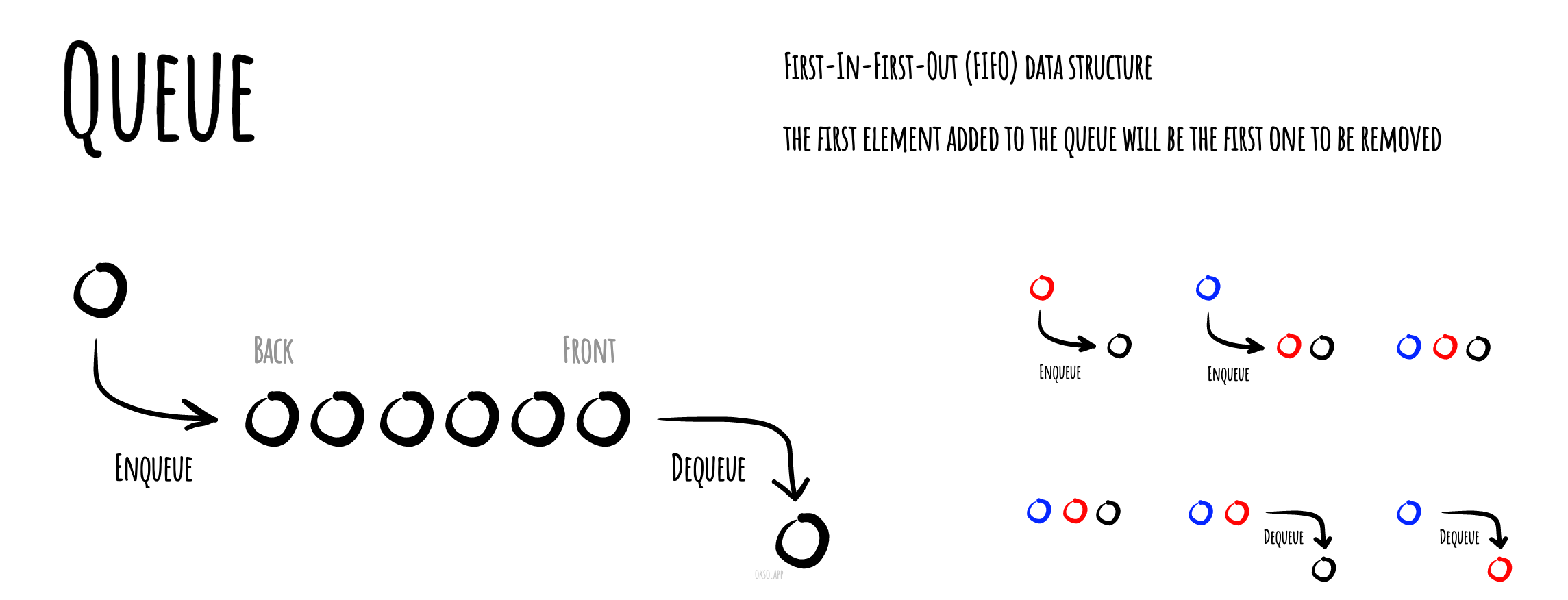
H2Hash Table


H2Trie
The trie data structure, also known as a prefix tree, is a tree-like data structure used for efficient retrieval of key-value pairs. It is commonly used for implementing dictionaries and autocomplete features, making it a fundamental component in many search algorithms.
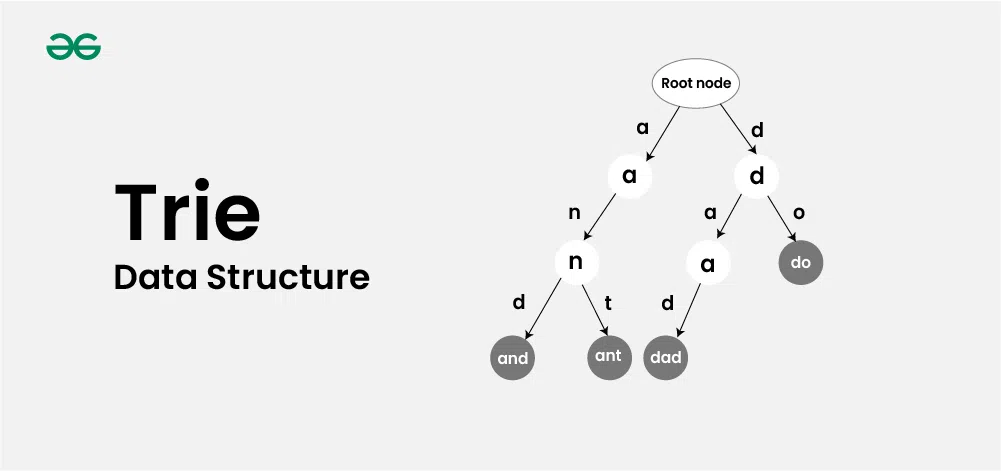
H2Tree
Tree Data Structure is a hierarchical data structure in which a collection of elements known as nodes are connected to each other via edges such that there exists exactly one path between any two nodes.
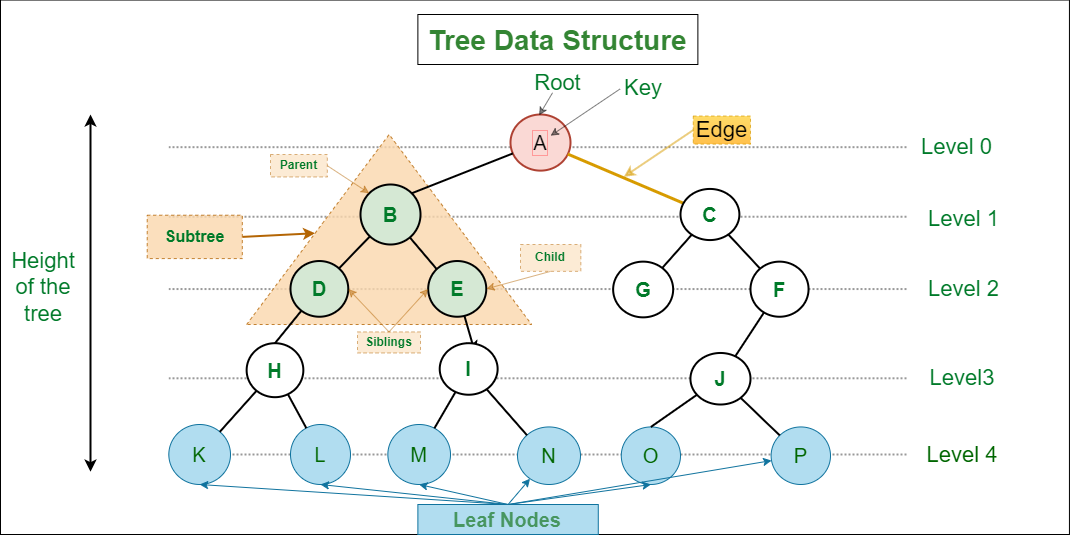
- Parent Node
- Child Node
- Root Node
- Leaf Node or External Node
- Ancestor of a Node
- Descendant
- Sibling
- Level of a node
- Internal node: A node with at least one child is called Internal Node.
- Neighbor of a Node: Parent or child nodes of that node are called neighbors of that node.
- Subtree
- Number of edges: An edge can be defined as the connection between two nodes. If a tree has N nodes then it will have (N-1) edges. There is only one path from each node to any other node of the tree.
- Depth of a node: The depth of a node is defined as the length of the path from the root to that node. Each edge adds 1 unit of length to the path. So, it can also be defined as the number of edges in the path from the root of the tree to the node.
- Height of a node: The height of a node can be defined as the length of the longest path from the node to a leaf node of the tree.
- Height of the Tree: The height of a tree is the length of the longest path from the root of the tree to a leaf node of the tree.
- Degree of a Node: The number of children of a node. The degree of a leaf node must be *0*. The degree of a tree is the maximum degree of a node among all the nodes in the tree.
H3Binary Tree
A Binary Tree is a non-linear data structure in which a node can have either 0, 1 or maximum 2 nodes. Each node in a binary tree is represented either as a parent node or a child node. There can be two children of the parent node, i.e., left child and right child.
H3Binary Search Tree
A Binary Search Tree is a tree that follows some order to arrange the elements, whereas the binary tree does not follow any order. In a Binary search tree, the value of the left node must be smaller than the parent node, and the value of the right node must be greater than the parent node.
H3Tree Traversal
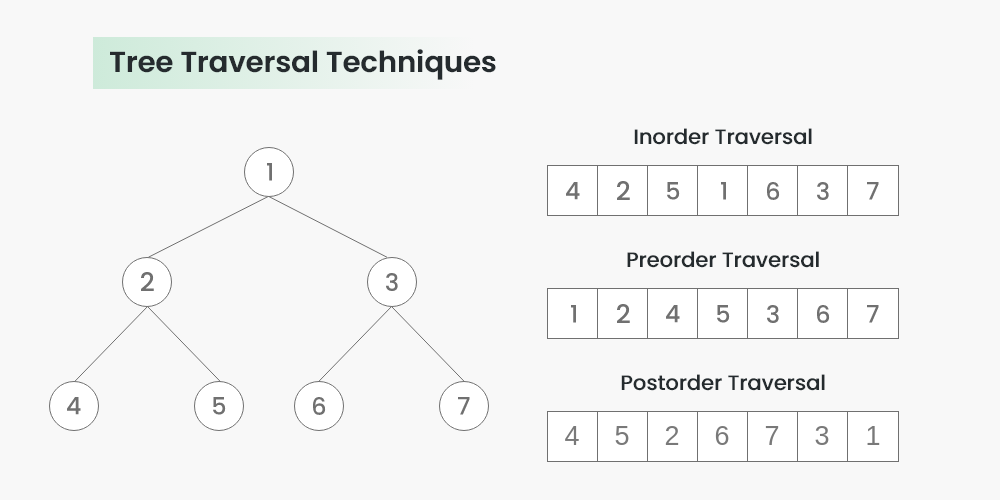
H2Graph
Graph Data Structure is a collection of nodes connected by edges. It’s used to represent relationships between different entities. Graph algorithms are methods used to manipulate and analyze graphs, solving various problems like finding the shortest path or detecting cycles.
H3Adjacency Matrix/List
It's a data structure used to represent a graph where each node in the graph stores a list of its neighboring vertices.
H3Detect cycle in an undirected graph
js
function test(nodeNum, nodeFrom, nodeTo) {
const adj = Array.from({ length: nodeNum + 1 }, () => new Set()),
v = new Set();
for (let i = 0; i < nodeFrom.length; i++) {
adj[nodeFrom[i]].add(nodeTo[i]);
adj[nodeTo[i]].add(nodeFrom[i]);
}
// Has Cycle?
const dfs = (node, prev) => {
v.add(node);
for (const n of adj[node]) {
if (!v.has(n)) {
if (dfs(n, node)) {
return true;
}
} else if (prev !== n) {
return true;
}
}
return false;
};
let min = 0;
for (let i = 1; i <= nodeNum; i++) {
if (!v.has(i) && !dfs(i, -1)) min++;
}
return min;
}H1Algorithms
H2Math
H3Euclidean Algorithm
In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the Greatest Common Divisor (GCD) of two numbers,
js
function EuclideanAlgorithmIterative (a, b) {
while (a && b) {
[a, b] = [b % a, a];
}
return a || b;
}H2Sliding Window
Sliding Window problems are problems in which a fixed or variable-size window is moved through a data structure, typically an array or string, to solve problems efficiently based on continuous subsets of elements. This technique is used when we need to find subarrays or substrings according to a given set of conditions.
.webp)
H2Boyer-Moore Voting Algorithm
It's used to find the majority element among the given elements that have more than N/ 2 occurrences. This works perfectly fine for finding the majority element which takes 2 traversals over the given elements, which works in O(N) time complexity and O(1) space complexity.
js
function findMajority(nums) {
var count = 0, candidate = -1;
// Finding majority candidate
for (var index = 0; index < nums.length; index++) {
if (count == 0) {
candidate = nums[index];
count = 1;
} else {
if (nums[index] == candidate) {
count++;
} else {
count--;
}
}
}
// Checking if majority candidate occurs more than N/2 times
count = 0;
for (var index = 0; index < nums.length; index++) {
if (nums[index] == candidate) count++;
}
if (count > (nums.length / 2))
return candidate;
return -1;
// The last for loop and the if statement step can be skip if a majority element is confirmed to be present in an array just return candidate in that case.
}
var arr = [ 1, 1, 1, 1, 2, 3, 4 ];
var majority = findMajority(arr);
document.write(" The majority element is : " + majority);H2Greedy Algorithm
A greedy algorithm is a type of optimization algorithm that makes locally optimal choices at each step with the goal of finding a globally optimal solution. It operates on the principle of “taking the best option now” without considering the long-term consequences.
Steps for Creating a Greedy Algorithm:
- Define the problem: Clearly state the problem to be solved and the objective to be optimized.
- Identify the greedy choice: Determine the locally optimal choice at each step based on the current state.
- Make the greedy choice: Select the greedy choice and update the current state.
- Repeat: Continue making greedy choices until a solution is reached.
H2Dynamic Programming
Dynamic Programming (DP) is a method used in mathematics and computer science to solve complex problems by breaking them down into simpler subproblems. By solving each subproblem only once and storing the results, it avoids redundant computations, leading to more efficient solutions for a wide range of problems.
How does dynamic programming (DP) work?
- Identify Subproblems: Divide the main problem into smaller, independent subproblems.
- Store Solutions: Solve each subproblem and store the solution in a table or array.
- Build Up Solutions: Use the stored solutions to build up the solution to the main problem.
- Avoid Redundancy: By storing solutions, DP ensures that each subproblem is solved only once, reducing computation time.
H2Backtracking Algorithm
Backtracking algorithms are like problem-solving strategies that help explore different options to find the best solution. They work by trying out different paths and if one doesn’t work, they backtrack and try another until they find the right one.
How Does a Backtracking Algorithm Work?
- Choose an initial solution.
- Explore all possible extensions of the current solution.
- If an extension leads to a solution, return that solution.
- If an extension does not lead to a solution, backtrack to the previous solution and try a different extension.
- Repeat steps 2-4 until all possible solutions have been explored.
H2Searches
H3Binary Search
In computer science, binary search, is a search algorithm that finds the position of a target value within a sorted array.
Time Complexity: O(log(n)) - since we split search area by two for every next iteration.
js
function binarySearch(arr, target) {
let start = 0, end = arr.length - 1;
while (start <= end) {
const middle = Math.floor((start + end) / 2);
if (arr[middle] === target) {
return middle;
} else if (arr[middle] > target) {
end = middle - 1;
} else {
start = middle + 1;
}
}
return -1;
}H3BFS
Breadth-first Search algorithm is used to search a tree or graph data structure for a node that meets a set of criteria. It begins at the root of the tree or graph and investigates all nodes at the current depth level before moving on to nodes at the next depth level.
H3DFS
Depth-First Search algorithm is a recursive algorithm that uses the backtracking principle. It entails conducting exhaustive searches of all nodes by moving forward if possible and backtracking, if necessary.
H2Sorting
H3Bubble Sort
O(n^2^)
js
const bubbleSort = (arr) => {
let isSwapped;
for (let i = 0; i < arr.length - 1; i++) {
isSwapped = false;
for (let j = 0; j < arr.length - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
isSwapped = true;
}
}
if (!isSwapped) break;
}
return arr;
}H3Insertion Sort
O(n^2^)
js
const insertionSort = (arr) => {
let i, j, curr;
for (i = 1; i < arr.length; i++) {
curr = arr[i];
j = i - 1;
while (j >= 0 && arr[j] > curr) {
arr[j + 1] = arr[j];
j--;
}
arr[j + 1] = curr;
}
return arr;
}H3Selection Sort
O(n^2^)
js
const selectionSort = (arr) => {
for (let i = 0; i < arr.length - 1; i++) {
let j = i, k = i + 1;
while (k < arr.length) {
if (arr[j] > arr[k]) j = k;
k++;
}
[arr[i], arr[j]] = [arr[j], arr[i]];
}
return arr;
}H3Quick Sort
O(n log(n))
js
const quickSort = (arr) => {
if (arr.length < 2) return arr;
const pivot = arr.pop(), left = [], right = [];
for (const item of arr) {
if (item < pivot) {
left.push(item);
} else {
right.push(item);
}
}
return [...quickSort(left), pivot, ...quickSort(right)];
}H3Merge Sort
O(n log(n))
js
const mergeSort = (arr) => {
if (arr.length < 2) return arr;
let len = arr.length, m = Math.ceil(len / 2);
let left = [], right = [], merge = [];
for (let i = 0; i < m; i++) left.push(arr[i]);
for (let i = m; i < len; i++) right.push(arr[i]);
left = mergeSort(left);
right = mergeSort(right);
let i = j = 0;
while (i < left.length && j < right.length) {
if (left[i] > right[j]) {
merge.push(right[j++]);
} else {
merge.push(left[i++]);
}
}
return [...merge, ...left.slice(i), ...right.slice(j)];
}H2Divide and Conquer
Divide and Conquer is a problem-solving strategy that involves breaking down a complex problem into smaller, more manageable parts, solving each part individually, and then combining the solutions to solve the original problem.
H1Notes
Setis more effcient thanArrayin terms of searching a certain element.Mapmay perform better thanObjectin scenarios where key-value pairs are frequently added or deleted.- Tree的DFS里,从根节点往子节点传递值的话,可以用放dfs函数的参数里;从子节点往根节点传递值,可以放dfs函数的return值里;
H1References
Videos:
Docs:





